|
|
Kleine Sachen mit PythonDas Acht-Damenproblem ⇓Noch'n Sudoku-Löser ⇓ |
|
|
Das Acht-Damenproblem
|
Die Aufgabe beim altbekannten Acht-Damenproblem ist es, acht Damen des Schachspieles so auf ein Schachbrett mit 8x8-Feldern aufzustellen, dass sie sich nicht gegenseitig schlagen können. Eine Dame zieht dabei horizontal in einer Zeile, vertikal in einer Spalte und diagonal auf der Haupt- und Nebendiagonalen bis zum letzten Feld am jeweiligen Brettrand. Das Problem kann man zu einem N-Damenproblem auf NxN-Feldern verallgemeinern. Das Problem lässt mit Pythonmitteln elegant mit wenigen Zeilen lösen. Der rekursive Algorithmis liefert im Prinzip alle Lösungen für ein gegebenes N. Einige Erläuterungen zum Python-Code: 1) Die Funktion fzelle(i,k) gibt einfach ein Zweiertupel zurück. Die Funktion sindBedroht(zelle1,zelle2) überprüft, ob zwei Damen in zwei Zellen sich einander bedrohen. Liegen die Zellen in einer Spalte, auf einer Nebendiagonalen, auf einer Hauptdiagonalen oder in einer Reihe? 2) Die Funktion istVertraeglichMit(damenListe,zelle) überprüft, ob eine neue Zelle verträglich ist mit einer Liste von Damenpositionen. Eine Damenposition ist ein Tupel (i,k) für die Reihe i und die Spalte k. Die Damenpositionen in der Liste sind selbst untereinander verträglich, sie bedrohen sich also gegenseitig nicht und stellen damit eine Zwischenlösung dar. Die Funktion verwendet eine sogenannte Listencomp (list comprehension). Diese hat hier den Aufbau ergebnisListe=[f(elem) for elem in elemListe], wobei für jedes Element elem der Liste die Funktion f(elem) berechnet wird, das Ergebnis wird der ergebnisListe hinzugefügt. Der Iterator reduce aus dem Modul functools iteriert kumulierend über die Liste istSicher und führt dabei die genannte lambda-Funktion aus; für eine Liste [b1,b2,b3,b4] mit 4 boolschen Werten wird dann der Ausdruck (((b1 and b2) and b3) and b4) berechnet und zurück gegeben. |
 |
|
3) Die Funktion nDamenProblem(anzahlDamen) ruft die Hilfsfunktion setzeDame(reihe) mit der Anzahl der gewünschten Damen auf. 4) Die Hilfsfunktion setzeDame(reihe) ruft für die Fälle reihe>0 mit setzeDame(reihe-1) sich selbst wieder auf. Im Fall reihe==0 gibt es keine Lösung und die leere Liste [] wird in einer Liste zurück gegeben. Die Funktion verwendet wieder eine Listencomp. Diese hat hier den Aufbau
ergebnisListe=[f(elem1,elem2) for elem1 in elemListe1
Es wird geschachtelt iteriert, die elem1-Schleife ist die äußere, die elem2-Schleife die innere Schleife. Die Funktion f(elem1,elem2) wird nur dann ausgeführt, wenn der Bedingungsausdruck hinter dem if erfüllt ist, wenn also gilt: bedingung(elem1,elem2)==True. Die Funktion setzeDame(reihe-1) gibt beim Erstaufruf alle bisher möglichen Zwischenlösungen für die ersten (anzahlDamen-1) Damen zurück. Dann wird für die letzte Spalte (und für alle bisherigen Zwischenlösungen) überprüft, ob die Spaltenzellen jeweils verträglich sind mit der gerade betrachteten Zwischenlösung. Wenn dieses für eine Zelle der Fall ist, wird die Zelle mit loesung+[(reihe,spalte)] zur Lösung hinzugefügt. Wenn keine der Spaltenzellen verträglich mit der gerade betrachteten Zwischenlösung ist, wird diese auch nicht der Ergebnisliste angehängt und wird somit verworfen. Wie startet die Rekursion am Ende der Aufrufkette? Beim Schritt reihe==0 mit der leeren Lösung [[]], beim zweiten Schritt mit der Lösungsliste (für 8 Damen): [[(1,1)],[(1,2)],[(1,3)],[(1,4)],[(1,5)],[(1,6)],[(1,7)],[(1,8)]], denn es gilt ja istVertraeglichMit([],zelle)==True für all diese Zellen. |
|
Etwas Testerei |
|
|
Mit 'Anzahl' ist hier die Anzahl der gefundenen Lösungen gemeint. Das Programm läuft natürlich nur auf einem Prozessorkern, man bräuchte einen Algorithmus, der sich leicht parallelisieren lässt. Rekursive Algorithmen scheinen da wenig geeignet zu sein. |
# Beginning Test ...
N: 1 | Anzahl: 1 # Finished Test. |
|
Lösungen N=5 |
Spiegellösung |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 1), (2, 3), (3, 5), (4, 2), (5, 4)]
|
[(1, 5), (2, 3), (3, 1), (4, 4), (5, 2)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 2), (2, 4), (3, 1), (4, 3), (5, 5)]
|
[(1, 4), (2, 2), (3, 5), (4, 3), (5, 1)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 3), (2, 1), (3, 4), (4, 2), (5, 5)]
|
[(1, 3), (2, 5), (3, 2), (4, 4), (5, 1)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 4), (2, 1), (3, 3), (4, 5), (5, 2)]
|
[(1, 2), (2, 5), (3, 3), (4, 1), (5, 4)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 5), (2, 2), (3, 4), (4, 1), (5, 3)]
|
[(1, 1), (2, 4), (3, 2), (4, 5), (5, 3)]
|
|
Lösungen N=6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 2), (2, 4), (3, 6), (4, 1), (5, 3), (6, 5)]
|
[(1, 5), (2, 3), (3, 1), (4, 6), (5, 4), (6, 2)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[(1, 4), (2, 1), (3, 5), (4, 2), (5, 6), (6, 3)]
|
[(1, 3), (2, 6), (3, 2), (4, 5), (5, 1), (6, 4)]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Da fällt doch gleich die strenge Regelmäßigkeit, die Symmetrien, der kleinen Lösungsmenge auf. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die Rekursionskette für N=6 |
|
# Beginning Test ...
1 1 |
Lösungen: [[(1 2), (2, 4), (3, 6), (4, 1), (5, 3), (6, 5)], [(1, 3), (2, 6), (3, 2), (4, 5), (5, 1), (6, 4)], [(1, 4), (2, 1), (3, 5), (4, 2), (5, 6), (6, 3)], [(1, 5), (2, 3), (3, 1), (4, 6), (5, 4), (6, 2)]] N: 6 | Anzahl: 4 # Finished Test. |
|
Ich habe zunächst gedacht, nur 4 Lösungen im Fall N=6, da kann doch etwas nicht stimmen! Warum gibt es etwa keine Lösung mit der Zelle (1,1)? Einige Beispiele zeigen, dass es keine Lösung zu geben scheint, wenn eine Diagonalzelle (blaues Kreuz) gesetzt ist. Man wird im Internet sicherlich etliche erschöpfende Ausführungen zum Damenproblem finden können. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quellcode für Python 3
Noch'n Sudoku-Löser — nachgebaut
|
Vor einiger Zeit trieb ich mich ein wenig in der rein funktionalen Programmiersprache Haskell herum. Haskell hat etwas, einen großen Reiz, Haskell ist elegant und bündig. Ich stolperte dabei über ein kleines, feines Haskell- Programm, Maggesi's Sudoku-Löser (http://web.math.unifi.it/users/maggesi/haskell_sudoku_solver.html) , das mich doch etliche Tage in den Bann zog nach dem Motto: Was passiert denn da in Gottes Namen nur? Ich habe es dabei für mich etwas Lesbarer gemacht und um Textausgaben erweitert: Maggesi's Sudoku-Löser. Python hat ja bei Haskell etliche Anleihen gemacht – was liegt näher, als einen kleinen prototypischen Löser in Python zu versuchen? |
|
|
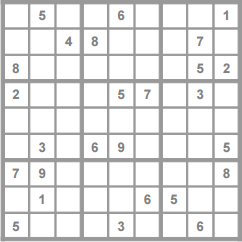
Das Rätsel Maggesi stellt das Sudoku-Spielfeld durch eine Funktion dar, ein Beispiel f : (1,2) → [7,8,9]. Ich mache es mir einfacher und nehme eine schlichte Datenstruktur, ein Zweiertupel aus den beiden Feldkoordinaten und einer Liste mit den möglichen Werten für das Feld, ein Beispiel ((1,2),[7,8,9]). |
|
|
|
|
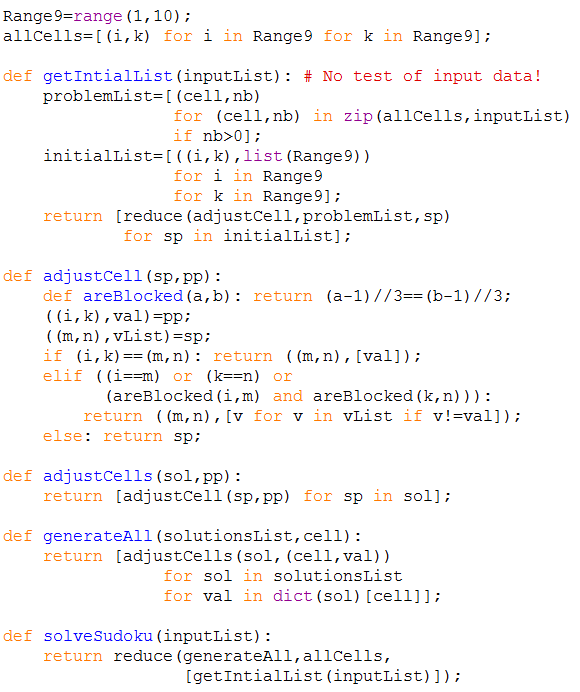
Der Algorithmus 1) getIntialList(inputList) Die Eingabeliste wird zunächst in eine Problemliste der Form [((1,2),5),((1,5),6),…,((9,8),6)] umgewandet, aus der ich die Initialliste erhalte, das ist eine Liste mit den möglichen Werten für jedes Sudoku-Feld. Die Python-Funktion zip (in Haskell: zip) fügt die Elemente zweier Listen elementweise zu einer neuen Liste von Zweiertupeln zusammen. Die Python-Funktion reduce (in Haskell: foldr) ist eine Faltungsfunktion, hier werden die Elemente einer Liste, hier problemList, mit Hilfe einer zweistelligen Funktion, hier das selbstdefinierte adjustCell, mit einem Startwert beginnend, hier sp, zusammengefasst. Ein Beispiel: reduce(lambda x,y:x+y,[1,2,3,4],0) berechnet ((((0+1)+2)+3)+4). Die Funktion ist hier einfach die normale Addition. Die Funktion verwendet Listencomps (list comprehensions), die Python auch von Haskell übernommen hat. Ein Beispiel: [k*k for k in [1,2,3,4,5,6] if k%2==0] erzeugt die Liste [4,16,25,36], der Operator % berechnet den Rest einer Dividion: 7%2=1.
Die Elemente der Initialliste haben zunächst für alle Felder
die Gestalt |
|
|
2) adjustCell(sp,pp) Diese Funktion wendet die Sudoku-Regeln auf eine Zelle oder Feld an und löscht entsprechend aus der Werteliste vList den Wert val. |
|
|
3) adjustCells(sol,pp) Diese Funktion wendet adjustCell auf eine Zwischenlösungliste sol an. sol ist eine Liste von Zweiertupeln aus Koordinatenpaaren und möglichen Feldwerten. |
|
|
4) generateAll(solutionsList,cell) Diese Funktion wendet adjustCells auf eine Liste von Zwischenlösungslisten solutionsList an. Die aktuelle Lösungsliste sol ist eine Liste von Zweiertupeln, jeweils bestehend aus der Zelle und den möglichen Zellenwerten. dict(sol) macht daraus ein Wörterbuch (dictionary), dict(sol)[cell] liefert die möglichen Zellenwerte für die Zelle. |
|
|
5) solveSudoku(inputList) Die Hauptroutine. Die Funktion erzeugt im Prinzip alle Lösungen des Sudoku-Rätsels ausgehend von der Liste, die die Initialliste enthält. Die Funktion generateAll schnappt sich den Initialwert [initialList] und das erste Element von allCells und wird ausgeführt; die zurück gegebene Ergebnisliste wird zusammen mit den zweiten Element von allCells für den nächsten Aufruf von generateAll verwendet, und so fort, bis auch das letzte Element von allCells verarbeitet worden ist. Man erhält eine Liste von Lösungen; die Liste ist leer, wenn es keine Lösung gibt. Prachtvoll! |
|
 |
|
|
Die Lösung Die eine Lösung für das verwendete Sudoku-Rätsel. Das Haskell-Programm konstruierte die gleiche Lösung. |
|

|
|

|
|
|
Einblicke |
|
|
Die vollständige Initialliste: Die gesetzten Felder sind blau gekennzeichnet. |
Die Anzahl der Zwischenlösungen für jeden Iterationsschritt: |
|
# Beginning Test ...
|
# Beginning Test …
|
|
Wird die 5 in der ersten Zeile im Feld (1,2) nicht gesetzt, so werden nach einer kleinen Zeit 55 Lösungen gefunden. |
# Beginning Test .. |
|
Wird zusätzlich im Ausgangsrätsel im Feld (7,5) eine 1 gesetzt, wird keine Lösung gefunden. |
# Beginning Test ... |
|
Anmerkung Der angegebene Algorithmus ist natürlich nur programmiertechnisch elegant, er findet einfach nur alle Lösungen und ist an keiner Stelle zeitlich optimiert oder lösungstechnisch trickreich. Es kam mir auf die schlichte Eleganz an, wie sie ja auch (noch im größeren Maße) das Maggesi-Programm in Haskell zeigt. |
|
Quellcode für Python 3
|
|
||
| © 2015 Bernd Ragutt
Alle Rechte vorbehalten |

|
letzte Änderung: 22. Februar 2018 Kruschtkiste |
|
|
||