Kalman-Filtern auf der Wanderung
Schlaue Algorithmik
»Ein Ausreißer Problem beim GPS-Navigieren«
Numerisch gelöst und animiert mit dem
Werkzeugkasten SciLab
Der Alltag
Auf weiten Wanderungen zeichnet das GPS-Gerät natürlich die Wegspur auf, man will ja wissen, wo man überall herum gelaufen ist und sich die Wanderung auch noch einmal auf der Landkarte anschauen.
Und? Die aufgezeichneten Daten weisen häßliche Ausreißer auf, die die Tourendaten verfälschen – die Empfangsqualität der GPS-Signale ist halt nicht immer und überall gleich gut. Ich als Wanderer weiß aber, dass ich von einer Sekunde auf die andere nicht 200 Meter weiter weg sein kann. Dummes Gerät!
Die Lösung? Man könnte etwa aus der augenblicklichen Wandergeschwindigkeit den nächsten Standort vorausberechnen und diesen Wert mit der fehlerbehafteten Position korrelieren, die aus den GPS-Daten ermittelt wird.
Ganz einfach? 'Tracking'-Algorithmen bei Radar-System arbeiten mit sogenannten Kalman-Filtern. Und die wollte ich ausprobieren!
Die Referenz
Ich hielt mich dabei an einem skizzierten Beispiel (Problem 5.2) in dem Buch:
Robert Grover Brown, Patrick Y. C. Hwang
Introduction to Random Signals and Applied Kalman Filtering
John Wiley & Sons, Inc, 1997
Die Bewegungsgleichung
Ausgangspunkt der Betrachtung ist die eindimensionale Bewegungsgleichung, eindimensional, der Einfachheit halber
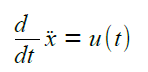
Die Zufallsfunktion u(t) stimuliert den Bewegungsablauf mit 'Weißem Rauschen'. Unter Weißem Rauschen versteht man einen stationären Zufallsprozess, der eine konstante spektrale Dichtefunktion aufweist. Die Autokorrelationsfunktion Ru für u(t) ist gegeben durch
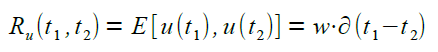
mit dem Erwartungswert E und der Diracschen Delta-Funktion, w ist eine Konstante, die angepasst werden muss.
Die Bewegungsgleichung
Die Autokorrelationsfunktion hängt nur von der Zeitdiffernz τ ab, der durch u(t) beschriebene Zufallsprozess ist damit stationär.
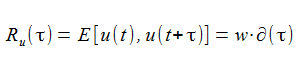
Die spektrale Dichtefunktion Su(iω) ist die Fourier-Transformierte der Autokorrelationsfunktion
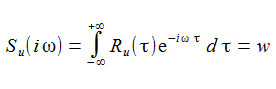
Das zeit-diskrete Modell
|
Das zeit-diskrete Modell wird durch die beiden Gleichungen definiert |
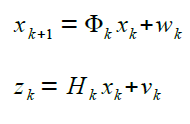
|
wobei die Größen die folgende Bedeutung haben
|
xk |
Zustandsvektor zur Zeit tk |
|
Φk |
Zustands-Überführungsmatrix, die tk mit tk+1 verknüpft |
|
wk |
Vektor, deren Komponten Zufallsvariablen sind |
|
zk |
Vektor mit den Messgrößen |
|
Hk |
Verbindungsmatrix zwischen den Meßgrößen und dem Zustandsvektor |
|
vk |
Vektor mit den Messfehlern, deren Kovarianz-Struktur bekannt sei |
Das zeit-diskrete Modell
|
Die Kovarianz-Matrizen für wk und vk sind: |
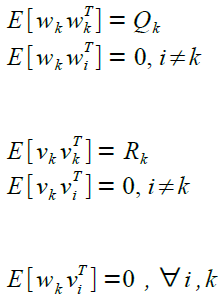
|
Mit Worten: Die Größen wk und vk sind jeweils für sich zeitlich unkorreliert. Und es gibt keine Kreuz-Korrelationen zwischen den Größen wk und vk.
Die zeit-diskrete Matrix-Gleichung
|
Die Differentialgleichung dritter Ordnung wird überführt in drei Differentialgleichungen erster Ordnung |
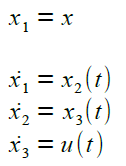
|
|
Das lässt sich wie folgt in Matrizenform schreiben |
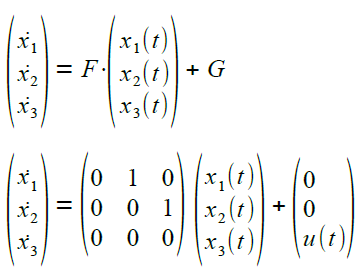
|
Die zeit-diskrete Matrix-Gleichung
|
Hieraus erhält man die diskretisierte Zustands-Überführungsmatrix Φk mittels der Gleichung |
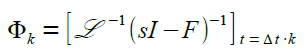
|
|
wobei der inverse Laplace-Operator zum Zuge kommt. Das Ergebnis sieht in zwei Schritten wie folgt aus: |
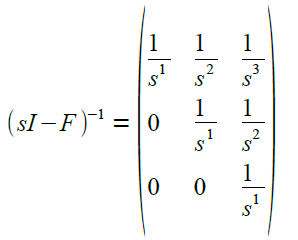
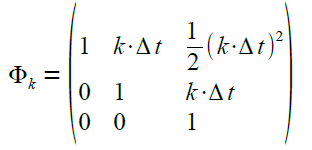
|
Die zeit-diskrete Matrix-Gleichung
|
Anstatt die Kovarianz-Matrix Qk über ihre Definition |
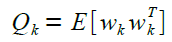
|
abzuleiten, folge ich den Ausführungen im genannten Buch und gehe von dem folgenden Blockdiagramm aus
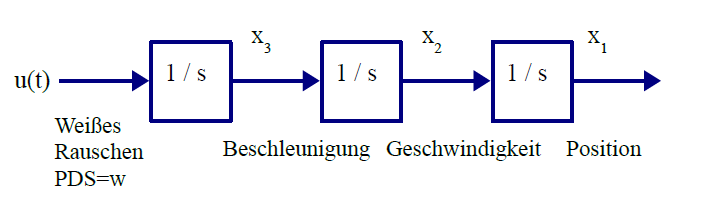
'PDS' steht für 'Power Spctral Density'. Dem Diagramm können wir direkt die Transfer-Funktionen entnehmen,
Die zeit-diskrete Matrix-Gleichung
|
G1 ist etwa die Transfer-Funktion von u nach x1 |
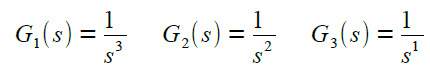
|
|
Die zu einer Transfer-Funktionen G(s) korrespondierenden Gewichtsfunktion g(t) ist definiert durch |
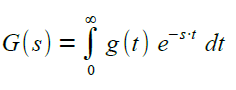
|
|
Man erhält dann |
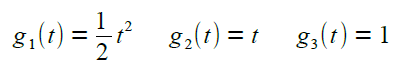
|
|
Mit diesen Funktionen berechnet man dann die Komponenten der Kovarianz-Matrix entsprechend der Formel |
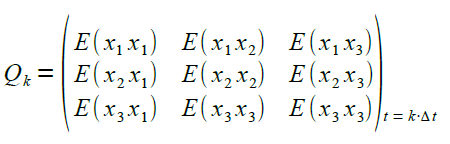
|
|
Ein Matrix-Element sei explizit berechnet |
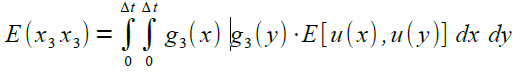
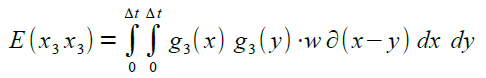
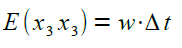
|
|
Die Kovarianz-Matrix Qk sieht dann am Ende wie folgt aus |
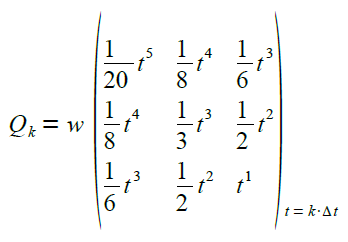
|
Hiermit sind alle Größen versamment, um den 'Kalman-Filter' füttern zu können.
Der diskrete Kalman-Filter
Die Matrizen-Gleichungen zum Kalman-Filter habe ich dem genannten Buch entnommen und sie Eins zu Eins in die Skriptsprache der Wissenschaftswerkbank SciLab übernehmen können.

Der diskrete Kalman-Filter
Die Matrizen-Gleichungen zum Kalman-Filter habe ich dem genannten Buch entnommen und sie Eins zu Eins in die Skriptsprache der Wissenschaftswerkbank SciLab übernehmen können.
|
Den vollständigen SciLab-Code habe ich in eine PDF-Datei gepackt und etwas aufgehübscht, Sie können ihn sich hier ansehen: |
Die Simulation
Den Formalismus in allen Ehren, man möchte natürlich aber auch etwas vor Augen haben und auch ein wenig herumspielen. So habe ich die Messungen simuliert und einige Ausreißer spendiert. Genaueres kann man dem beigefügten SciLab-Code entnehmen.
Hier nun einige Ergebnisse.
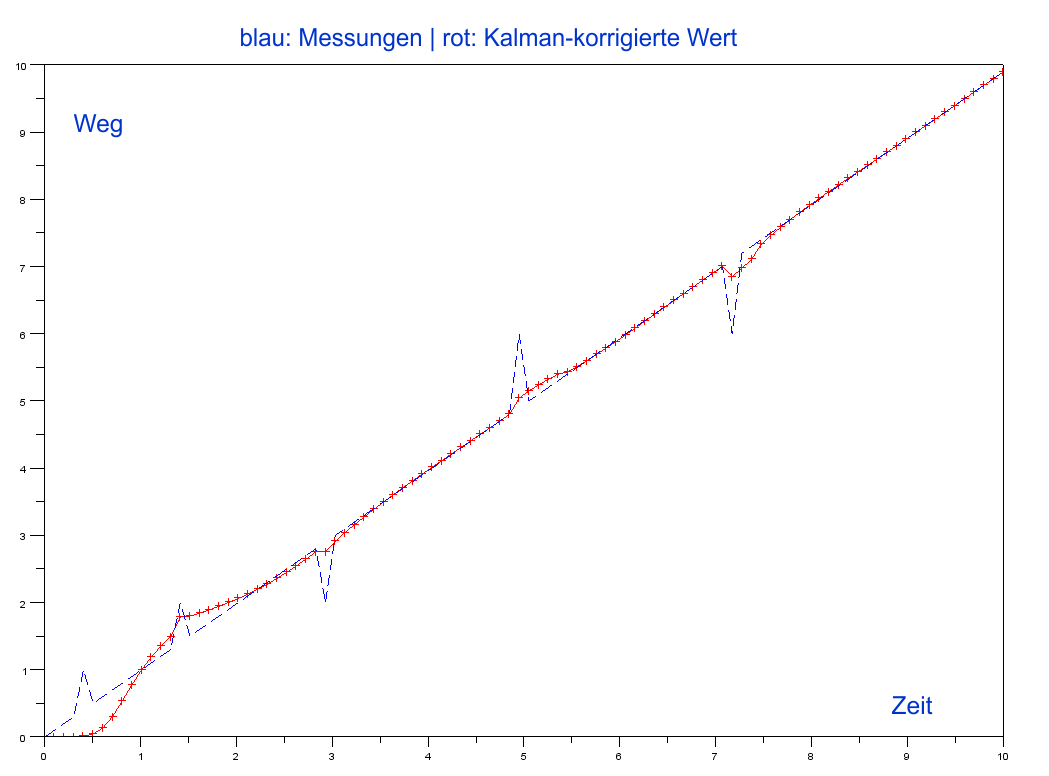
Man sieht, der 'Filter' muss sich anfänglich noch einschwingen, dann werden Ausreißer brav ausgemittelt.
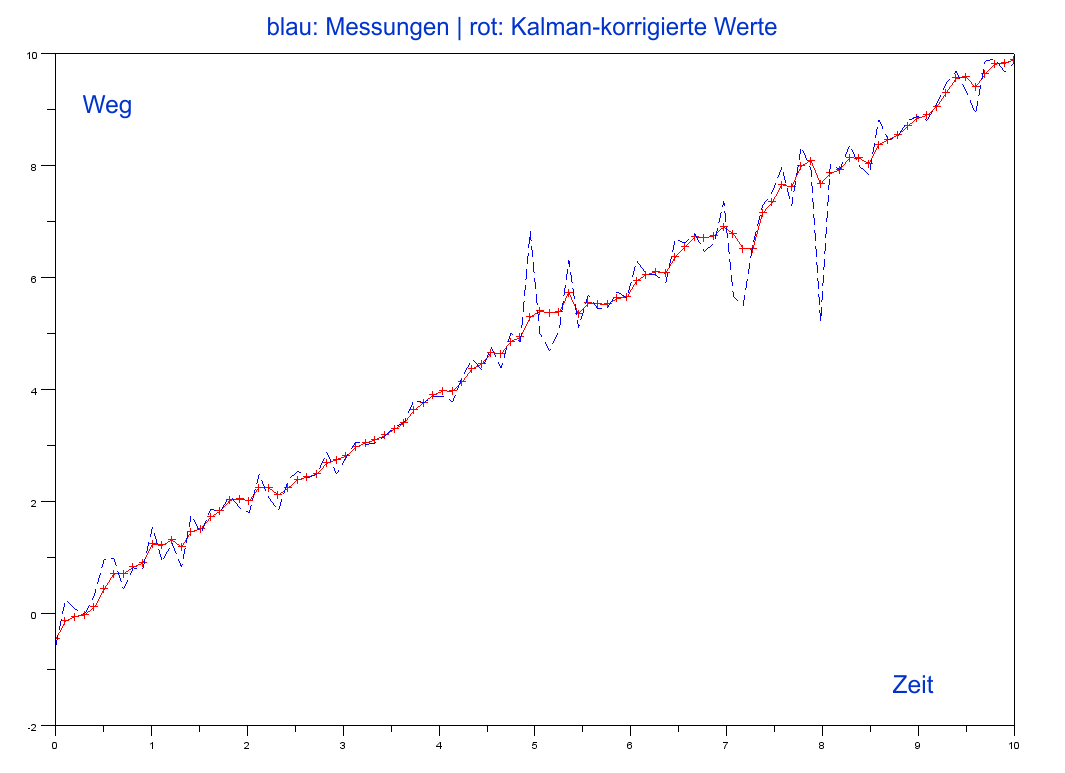
Hier eine Messreihe mit größeren Schwankungen, der 'Filter' wirkt wieder ausgleichend.
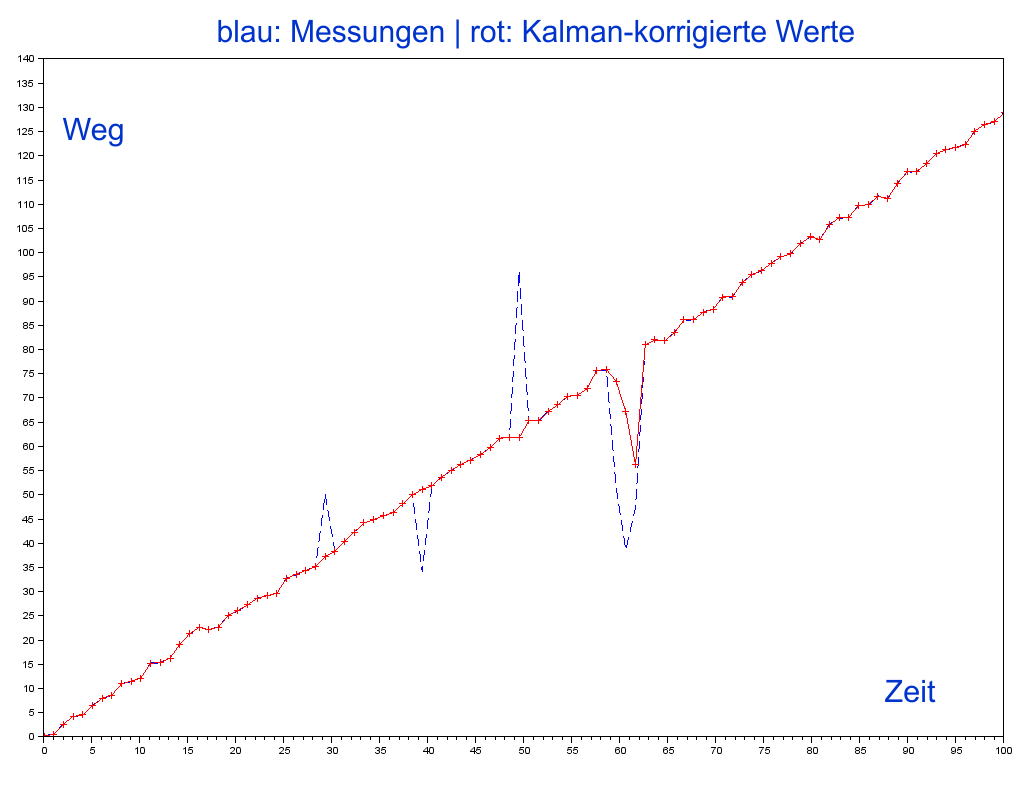
Halten die Ausreißer einige Zeit an, folgt der 'Filter'.
Beiträge
| Filtertheorie | R. E. Kalman, 1960 |
| Lehrbuch | R. G. Brown, P. Y. C. Hwang, 1997 |
| Werkzeug | SciLab |
| Webgerüst | impress |
| Foliensatz | Bernd Ragutt |
| Erstellt | Weihnachtszeit 2011 |
| Geändert | 19. September 2014 |