|
|
Das Foucault'sche Pendel |
|
|
|
|
|
Ein Hinweis: Das unten benutze ENU-Bezugssystem,
|
|
|
Die Newton'sche Bewegungsgleichung
|
Ein Pendel der Länge l und der Masse m schwingt im Schwerefeld der Erde. Das kartesische, mitrotierende Koordinatensystem {ei} befestige ich im Aufhängepunkt des Pendels. Die Masse m hat die Koordinaten xi (oder auch x,y,z). |
|
Die Newton'sche Bewegungsgleichung
Diese Bedingung wird durch eine Zwangskraft KZ, die senkrecht auf der Kugeloberfläche steht, in der Bewegungsgleichung berücksichtigt. λ ist der sogenannte Lagrange-Multiplikator, er muss besstimmt werden. |
|
|
Hinweis: Hier ist mir ein Lapsus passiert, der Vektor der Scheinkräfte KS muss ein negatives Vorzeichen tragen. Da bei den Betrachtungen auf dieser Seite nur die Corioliskraft als Scheinkraft auftritt, muss im folgenden Text überall ω durch -ω ersetzt werden, ansonsten würde die Ablenkung durch die Corioliskraft (nur) in die falsche Richtung erfolgen, auf der Nordhalbkugel dann nicht nach Osten sondern nach Westen. |
|
|
Multipliziert man die Bewegungsgleichung mit x, so erhält man den Lagrange-Multiplikator zu: Was hier passiert? Durch die Zwangskraft werden die radialen Komponenten der Kräfte ersetzt durch eine ebenfalls radiale Kraft, die die Pendelmasse auf der Kugeloberfläche hält. |
|
|
Ich vereinfache das Problem: Die Erde habe eine Kugelgestalt, die Gravitationsbeschleunigung sei konstant und ich lasse nur die Corioliskraft wirken. (Die Zentrifugalkraft kann an der Erdoberfläche vernachlässigt werden.) In einem ENU-Bezugssysystem auf Höhe der Breite ϑ sind dann die Beschleunigungen: Der konstante Vektor ω beschreibt die Erdrotation in Richtung und Winkelgeschwindigkeit. |
|
|
Es lässt sich der Energieerhaltungssatz mit den gegebenen Voraussetzungen ableiten:
|
|
|
Versucht man nun, diese Differentialgleichung mit dem SciLab-Integrator mit Brachialgewalt zu lösen, ergibt sich in der Tat eine Schwingungsbewegung, in meinem Beispiel liegt der Radius der Pendelbewegung in der Tat nahezu konstant bei 30 Meter und nimmt dann aber langsam mit der Anzahl der Integrationsschritte ab: |
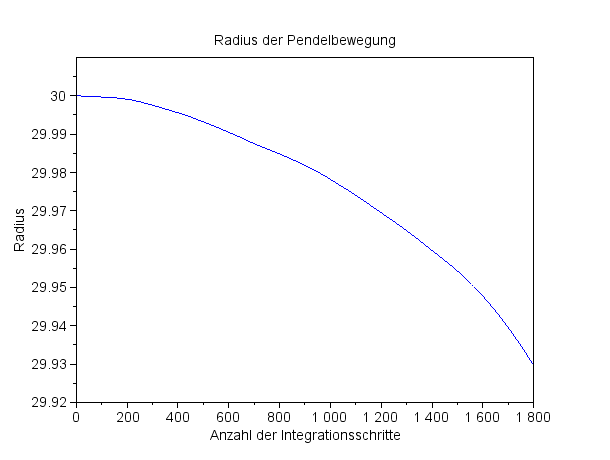
Radius der Pendelbewegung
|
Auch die Bedingung
Der Azimuthwinkel scheint langsam zu wachsen, es zeigen sich aber häßliche Ausreißer – ein deutlicher Hinweis, dass der Integration nicht ganz zu trauen ist (Grafik unten): |
+0.0009255 -0.0000099 -0.0000077
+0.1567990 +0.0481313 +0.0376043
|
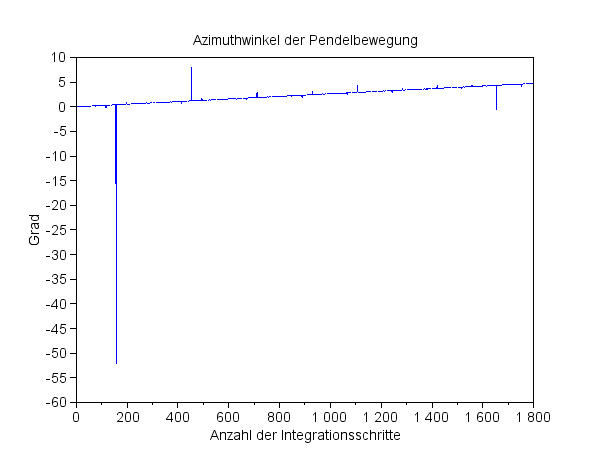
Azimuthwinkel der Pendelbewegung
| Quellcode für Scilab Verwendet wurde SciLab 5.4.1 (64-bit) |
|
|
Das Pendel in sphärischen Koordinaten
|
Ich führe im ENU-Bezugssystem {i=1,2,3} an der Breite ϑ sphärische Koordinaten {χ, γ, r} ein. Die vertikale 3-Achse zeigt zum Zenit, der Winkel γ (gamma) ist der Auslenkwinkel des Pendels gegenüber der Vertikalen entgegen dem Uhrzeigersinn, der Winkel χ (chi) ist der Azimuthwinkel. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Radialkomponenten sind nur der Vollständigkeit halber aufgenommen – sie werden ja durch die Zwangskraft kompensiert. Die Bewegungsgleichungen sind: |
|
|
|
|
|
|
|
|
Der Energiesatz ist: |
|
|
Der Drehimpuls ist: |
|
|
Das Drehmoment ist: |
|
|
|
|
|
Anmerkung: Eine Parametertransformation des Azimuthwinkels, die die Drehung der Pendelebene berücksichtigen sollte, blieb ohne Erfolg. Am Pol sah das Bild etwas anders aus, aber bei der Breite 89° stieg der Integrator aus. |
|
|
|
|
|
|
|
|
|
Das Pendel ohne Erdrotation
|
Die Bewegungsgleichungen mit ω=0 sind: |
|
|
|
|
|
Die Azimuthgeschwindigkeit ist also am größten, wenn das Pendel durch die Minimumlage schwingt. |
|
|
Die Lagrangefunktion LG=T-V ist: |
|
|
χ ist eine zyklische Variable. |
|
|
Die Energie E=T+V bleibt erhalten: |
|
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
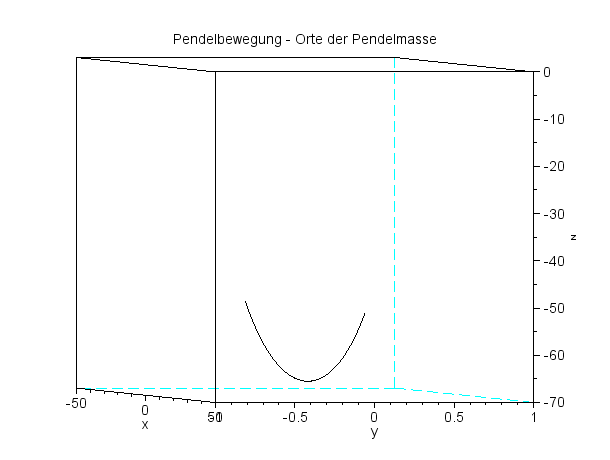
Das Pendel schwingt in einer Ebene
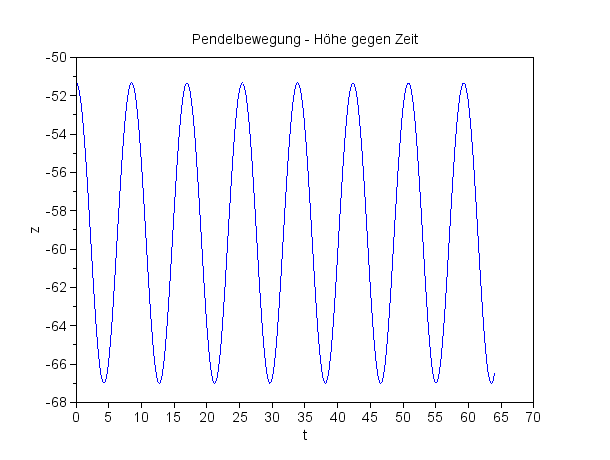
Es schwingt tatsächlich!
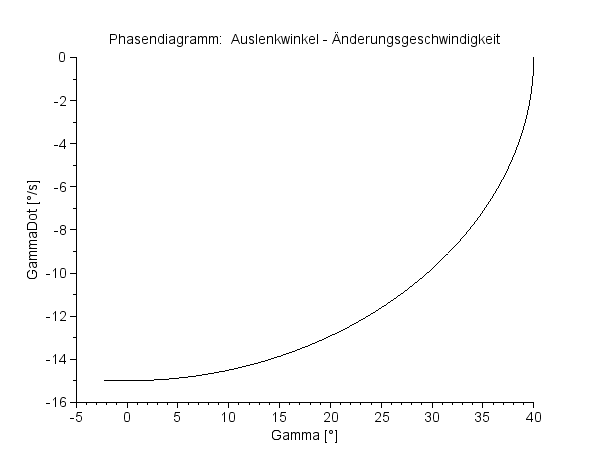
Phasendiagramm:
Auslenkwinkel – Änderungsgeschwindigkeit Viertelperiode
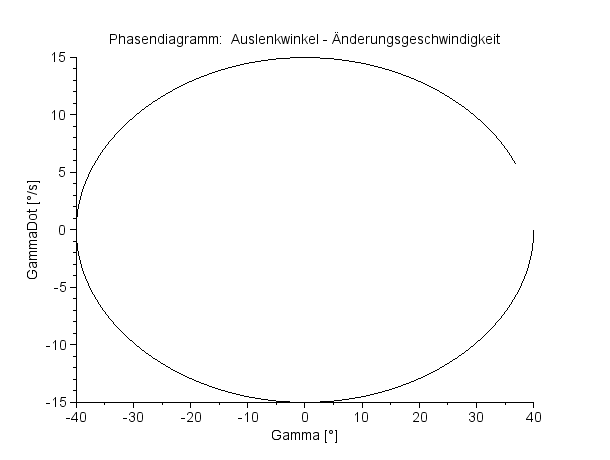
Phasendiagramm:
Auslenkwinkel – Änderungsgeschwindigkeit Vollperiode
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
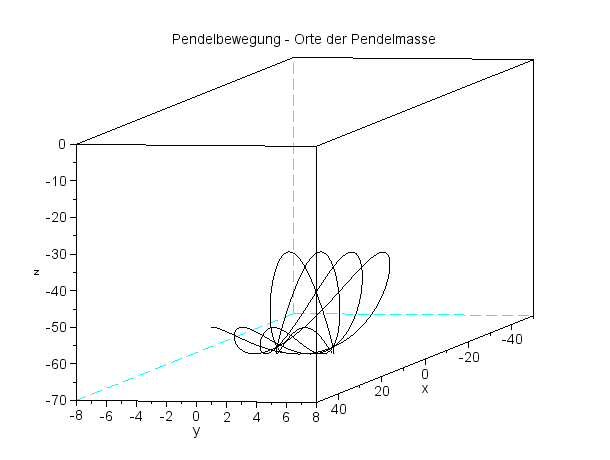
Mit einer kleine azimuthalen Anfangsgeschwindigkeit ...
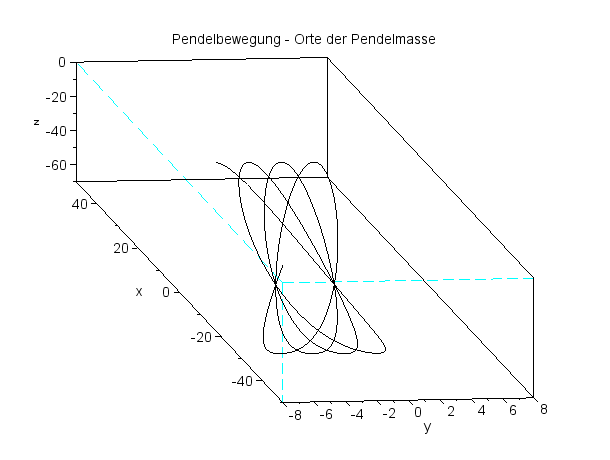
Ein schräger Blick von oben ...

Und mehr von der Seite ...
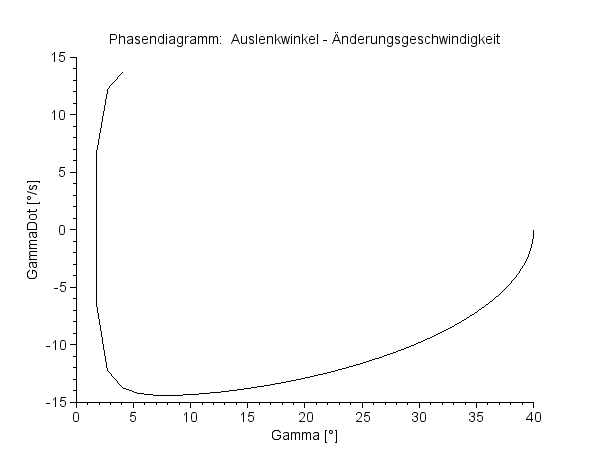
Phasendiagramm:
Auslenkwinkel – Änderungsgeschwindigkeit
Viertelperiode
|
Sobald
|
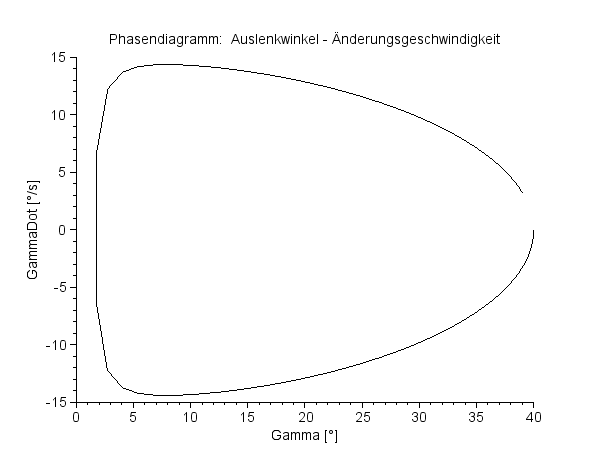
Phasendiagramm:
Auslenkwinkel – Änderungsgeschwindigkeit Vollperiode
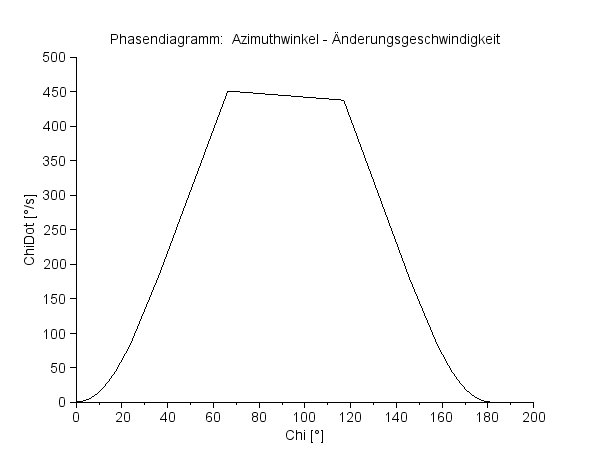
Phasendiagramm:
Azimuthwinkel – Änderungsgeschwindigkeit
Vollperiode
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
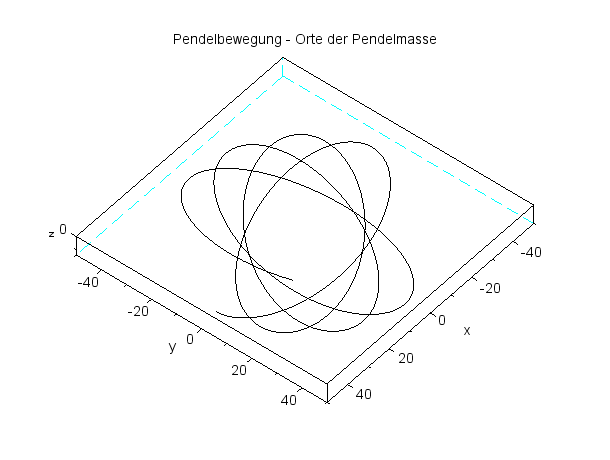
Schöne Figuren ...
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 640 s |
|
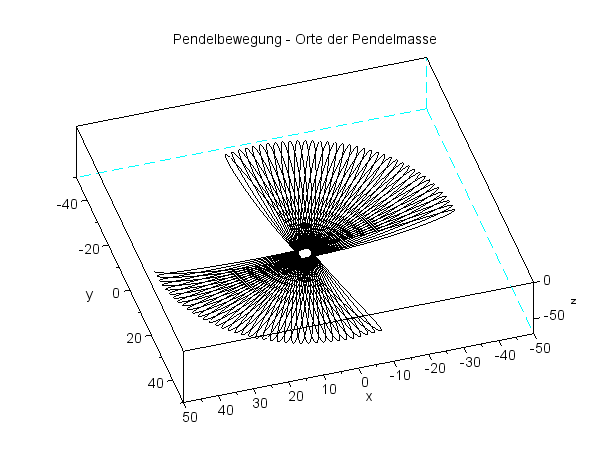
Das Pendel schwingt nun 640 s ...
|
Die Gesamtenergie bleibt über die Integrationszeit hinreichend konstant. (Maximalwert: -14084,516; Minimalwert: -14084,598) Die Änderungen bei der Gesamtenergie betreffen die sechste Stelle – und das ist gerade die Größenordnung des Corioliseffektes. |
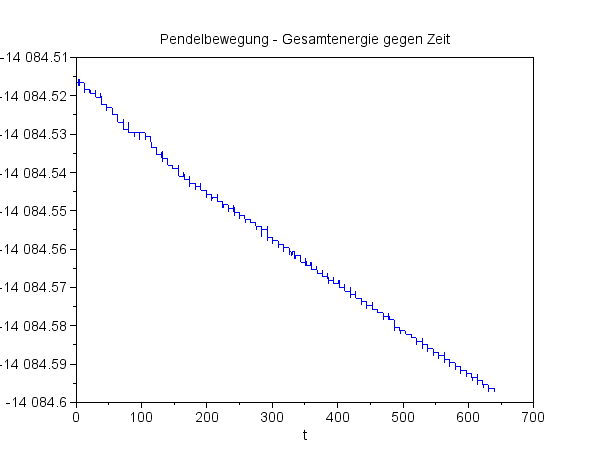
Die Gesamtenergie bleibt annähernd konstant
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
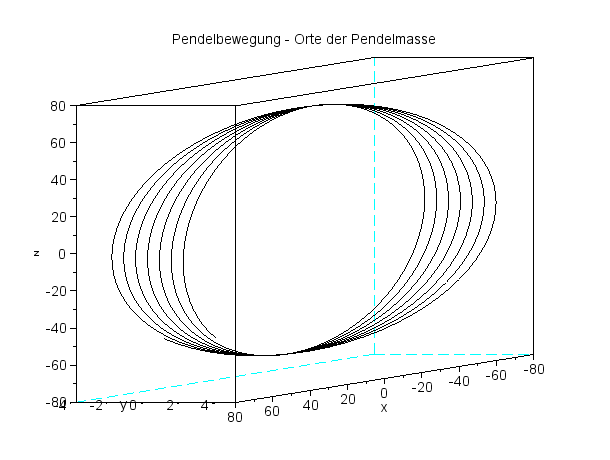
Vollkreise beim kräftigen Anstoß
|
|
Das Pendel mit Erdrotation
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
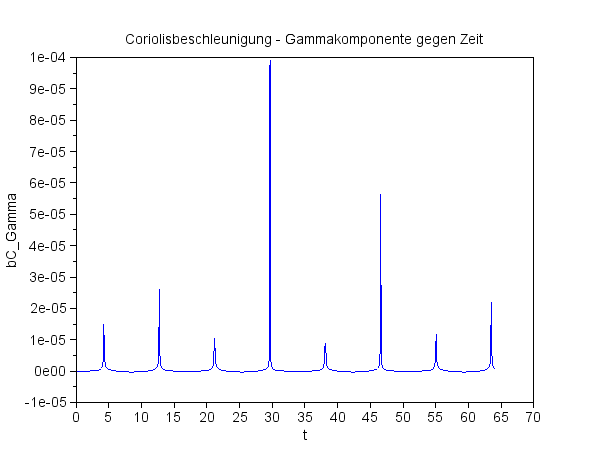
Die Gammakomponente der Coriolisbeschleunigung
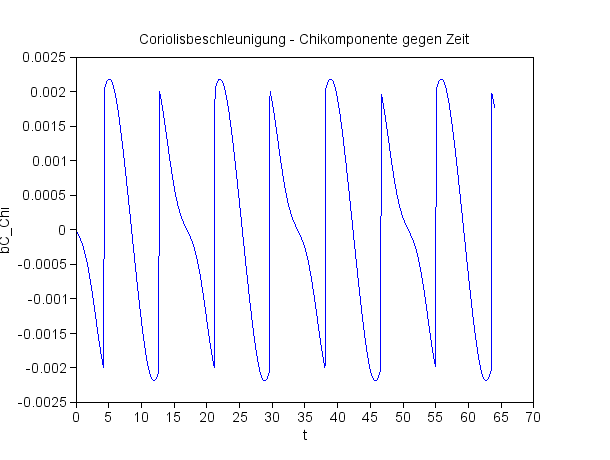
Die Chikomponente der Coriolisbeschleunigung
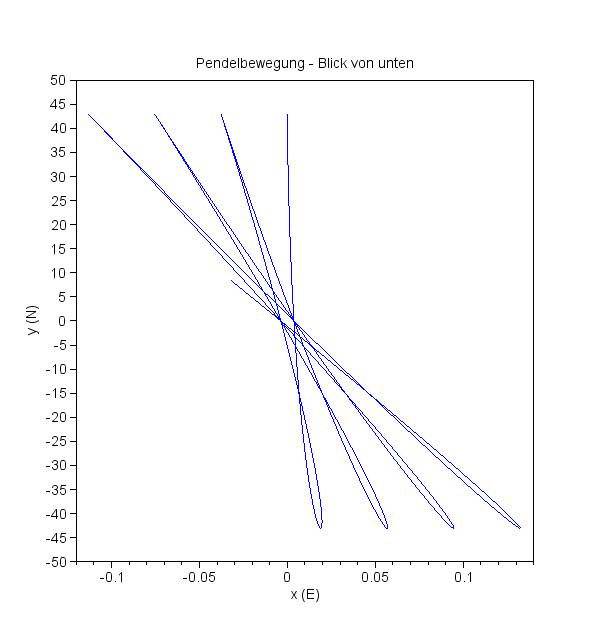
Die Schwingungsebene dreht sich
|
Man beachte die ganz unterschiedlichen Skalen der Achsen! Das Pendel schwingt anfänglich in der Ebene x=0. |
|
Breite 52° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
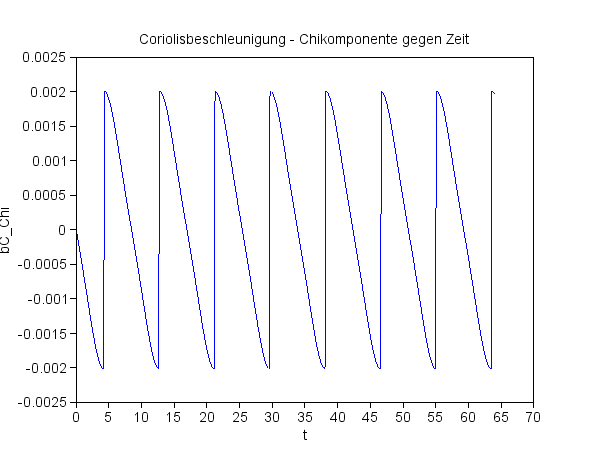
Die Chikomponente der Coriolisbeschleunigung
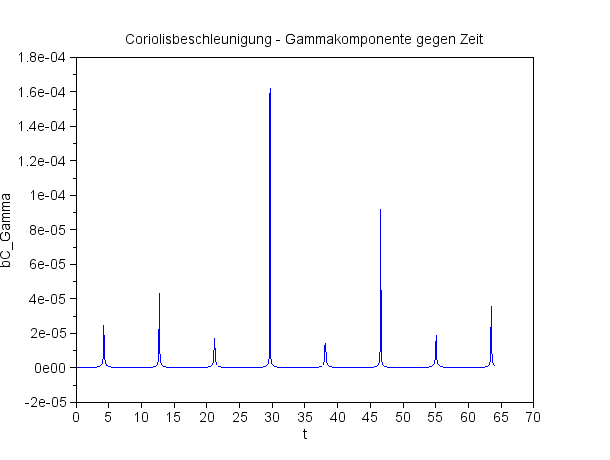
Die Gammakomponente der Coriolisbeschleunigung
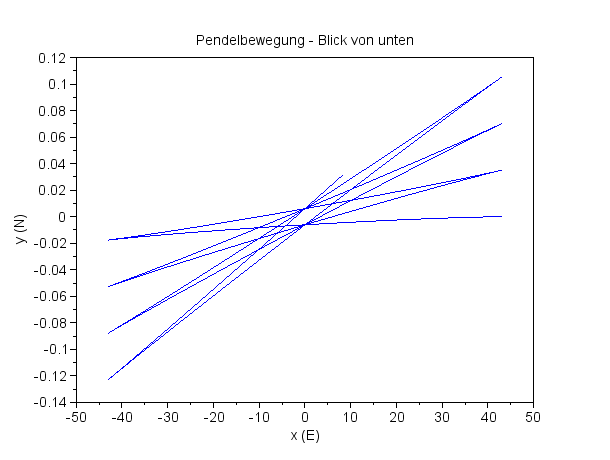
Die Schwingungsebene dreht sich
|
Man beachte die ganz unterschiedlichen Skalen der Achsen! Das Pendel schwingt anfänglich in der xz-Ebene (y=0). |
| Quellcode für Scilab Verwendet wurde SciLab 5.4.1 (64-bit) |
|
|
Das Pendel am Äquator
|
Die Bewegungsgleichungen am Äquator sind: |
|
|
|
|
|
Die Komponenten der Coriolisbeschleunigung am Äquator sind: |
|
|
Breite 0° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
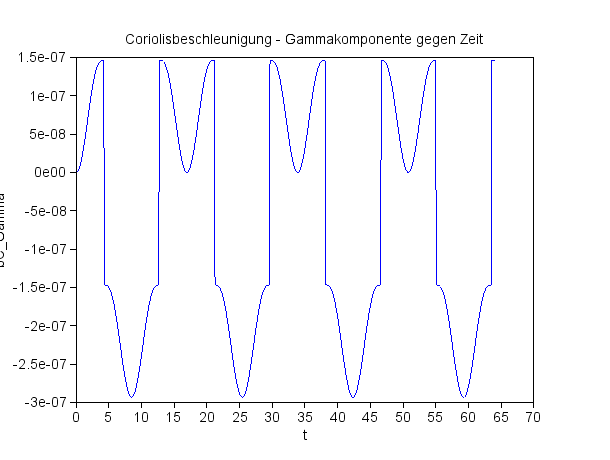
Die Gammakomponente der Coriolisbeschleunigung am Äquator
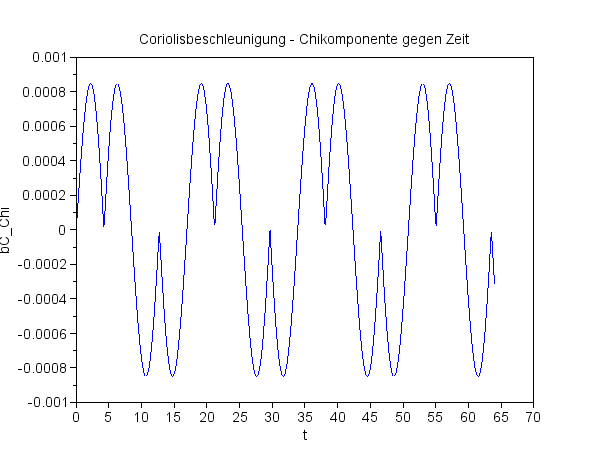
Die Chikomponente der Coriolisbeschleunigung
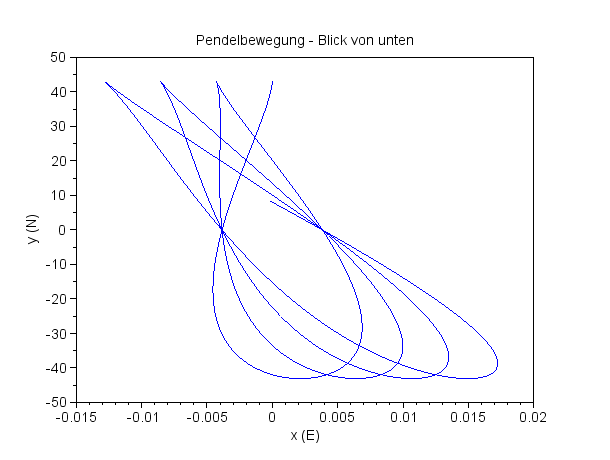
Ein kleiner, aber hübscher Effekt! Ewas unsymmetrisch, das Ganze ...
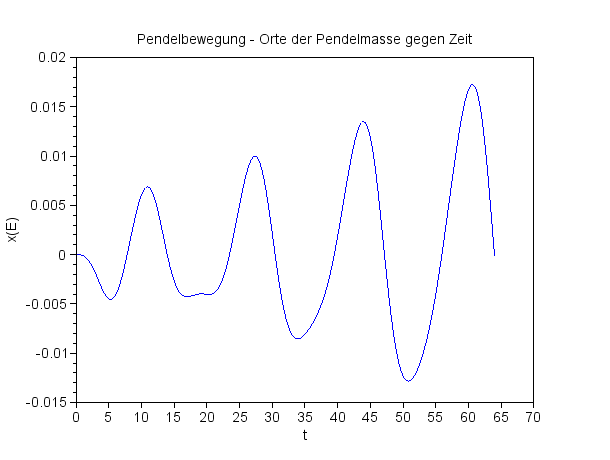
x-Koordinate der Pendelmasse gegen die Zeit
|
Es gibt eine leichte Asymmetrie ins Positive |
|
Breite 0° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
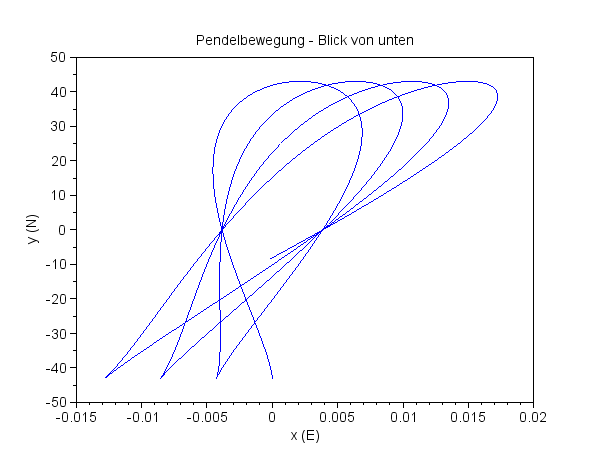
Eine kleine Umkehrung der Schwingungsrichtung
|
Breite 0° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
|
Gibt man der Pendelmasse eine Anfangsgeschwindigkeit auf dem Weg, so verschwinden die Spitzen, die Unstetigkeiten. |
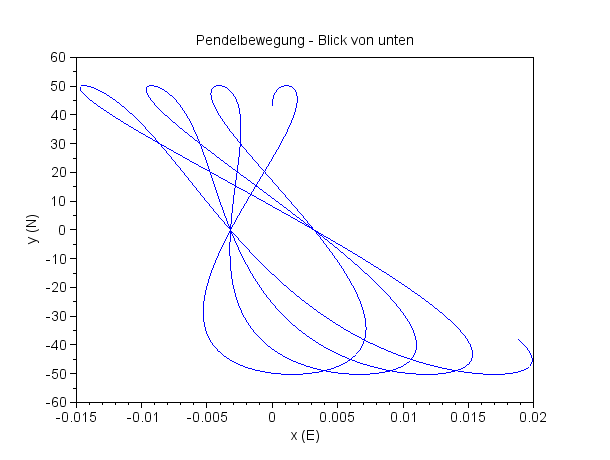
Nun mit einem kleinen Stups ...
|
Breite 0° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
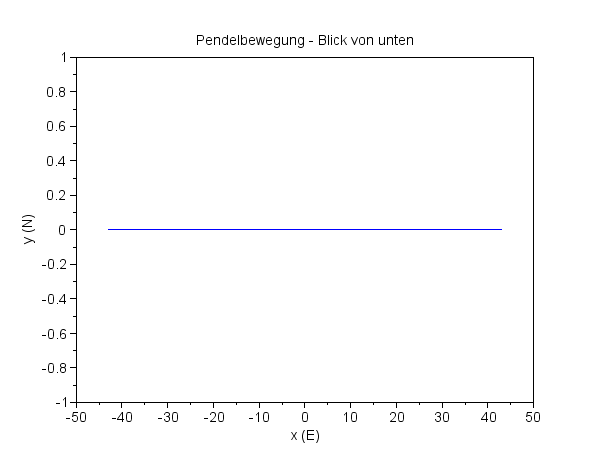
In y(N)-Richtung verschwindet die Coriolisbeschleunigung
|
Das Pendel schwingt anfänglich in der xz-Ebene und bleibt auch in dieser Ebene, denn die Coriolisbeschleunigung verschwindet (sinχ=0). |
|
|
Das Pendel am Pol
|
Die Bewegungsgleichungen am Pol sind: |
|
|
Daraus lässt sich eine
Konstante der Bewegung ableiten, die numerisch Werte der
Größenordnung 10-5
(für
|
|
|
Der Azimuthalbewegung ist also eine Rotation mit der Winkelgeschwindigkeit +ω überlagert. |
|
|
Die Komponenten der Coriolisbeschleunigung am Pol sind: |
|
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
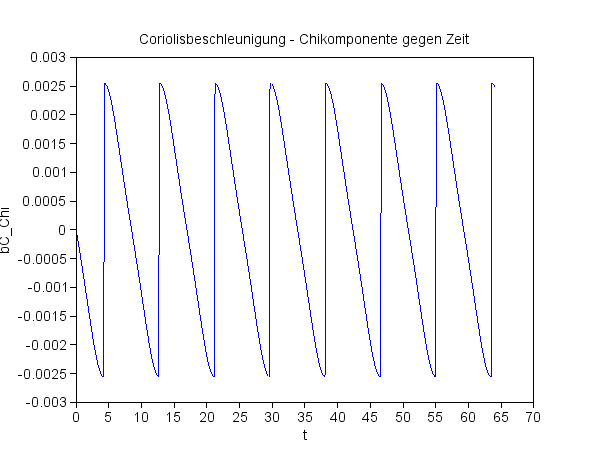
Die Chikomponente der Coriolisbeschleunigung am Pol
|
Am Pol ist die Coriolisbeschleunigung drei Mal größer als am Äquator, ihr Verlauf zeigt auch keine Substrukturen. |
|
Ein lineare Fit ergibt: Über alle Perioden gibt es einen sehr kleinen, negativen Beschleunigungswert für χ. |
y = -0,000.006.8 – 2,293D-09 *x |
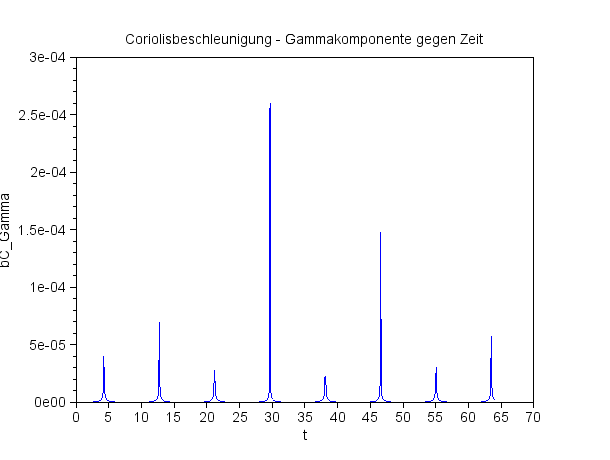
Die Gammakomponente der Coriolisbeschleunigung
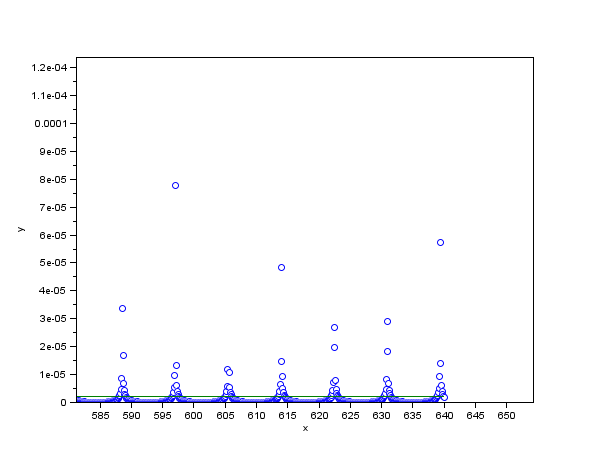
Ein linearer Fit für die Gammakomponente der Coriolisbeschleunigung
|
Der lineare Fit kommt als grüne Gerade daher: x meint die Zeit und y den Winkelwert in Radian. Über alle Perioden gibt es einen sehr kleinen, positiven Beschleunigungswert für Gamma. |
y = 0,000.002.6 – 1,006D-09 * x |
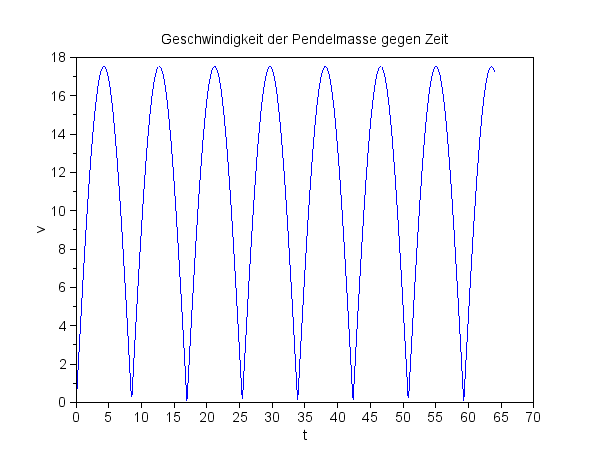
Gesamtgeschwindigkeit der Pendelmasse
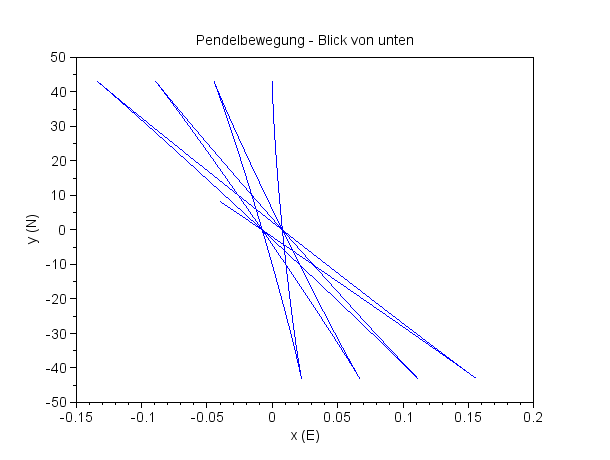
Eine saubere Drehbewegung
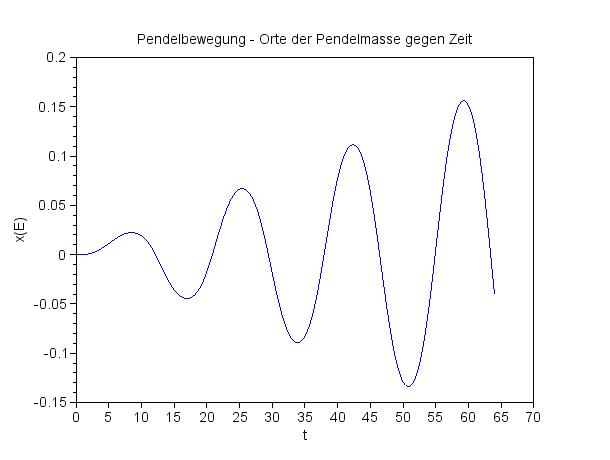
x-Koordinate der Pendelmasse gegen die Zeit
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
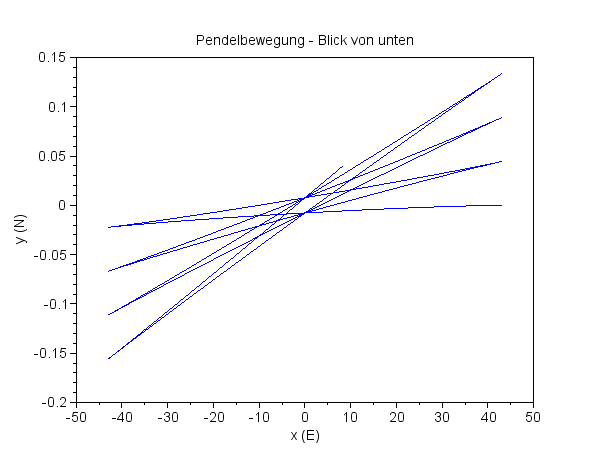
Keine Überraschung
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 640 s |
|
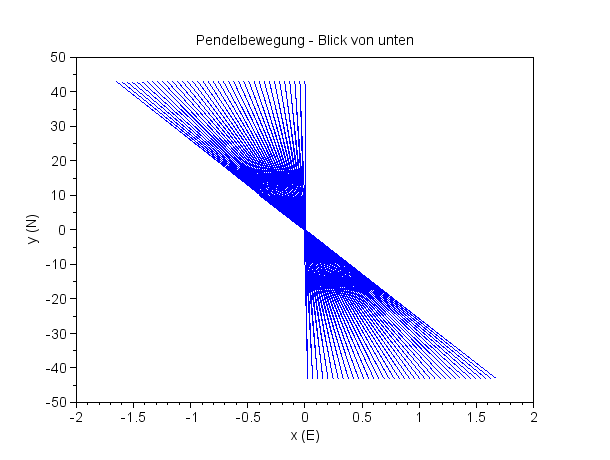
Und in 640 Sekunden ...
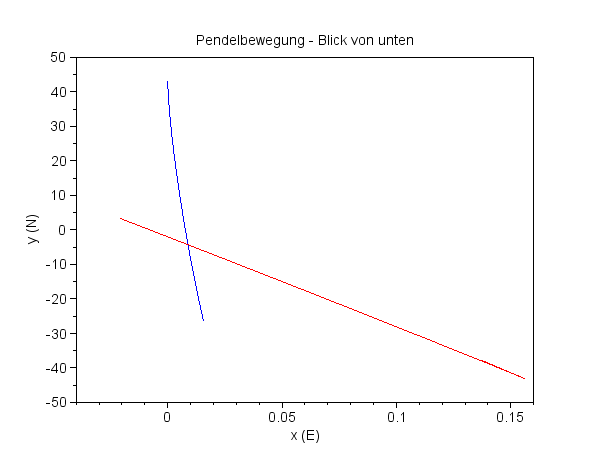
Anfang (blau) und Ende (rot) der 640 Sekunde
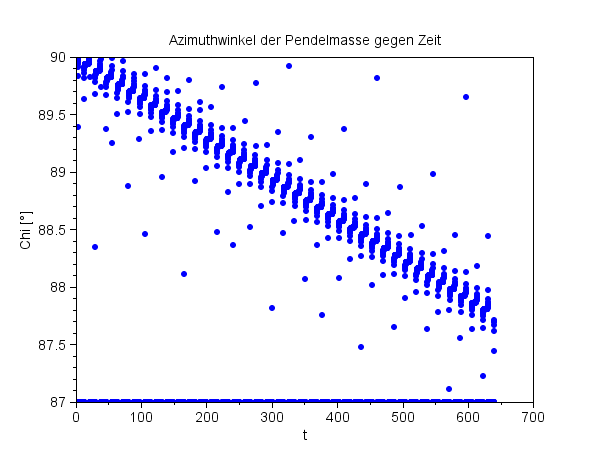
Bereinigter Azimuthwinkel in Grad
|
Die Hälfte der berechneten Azimuthwerte lag knapp unter -90° - weshalb habe ich (noch) nicht analysiert. Die negativen Werte und positive Ausreißer, die kleiner als 87° waren, habe ich auf den Wert 37° gesetzt. Am Pol dreht sich die Pendelebene in 10 Minuten genau um 2,5°. Die Grafik gibt diese Tendenz qualtitativ richtig wider, von einer numerischen Lösung kann aber keine Rede sein. |
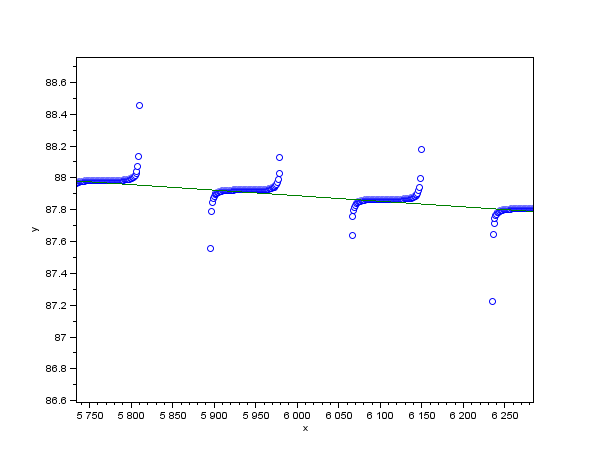
Linearer Fit für alle positiven Chi-Werte (Ausschnitt um 6000 s)
|
|
Was kann man glauben?
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s t0=0 tend=64 steps=641 |
|
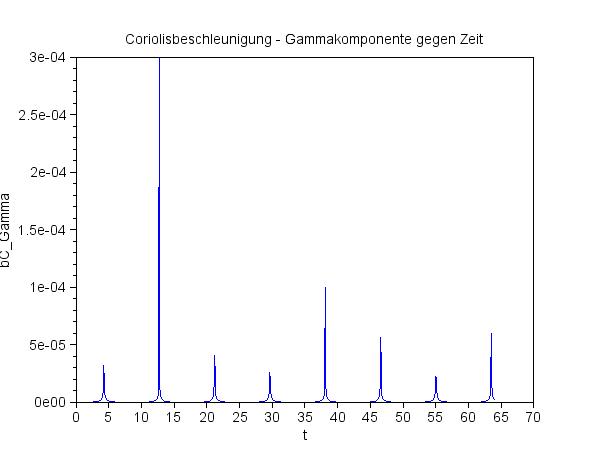
641 Intervalle beim Lösen der Differentialgleichung
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s t0=0 tend=64 steps=643 |
|
|
Die berechneten Werte der Gammakomponenter der Coriolisbeschleunigung verändern sich 'dramatisch', wenn die Anzahl der Integrationsschritte etwas verändert wird. Die Differentialgleichugen weisen Pole für γ=0 auf.
Ist der gewählte Anfangswert
Erst wenn
|
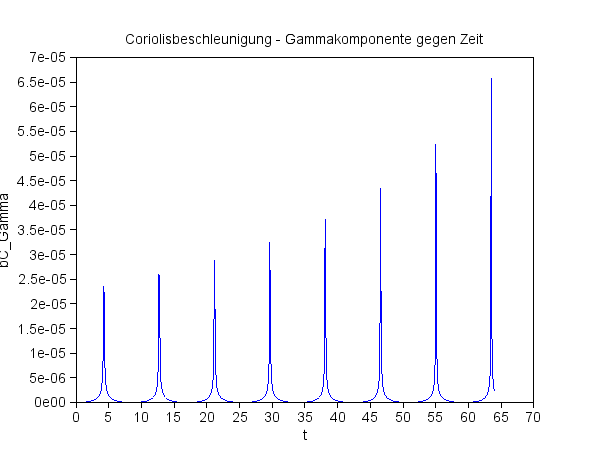
643 Intervalle beim Lösen der Differentialgleichung
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s t0=0 tend=64 steps=643 |
|
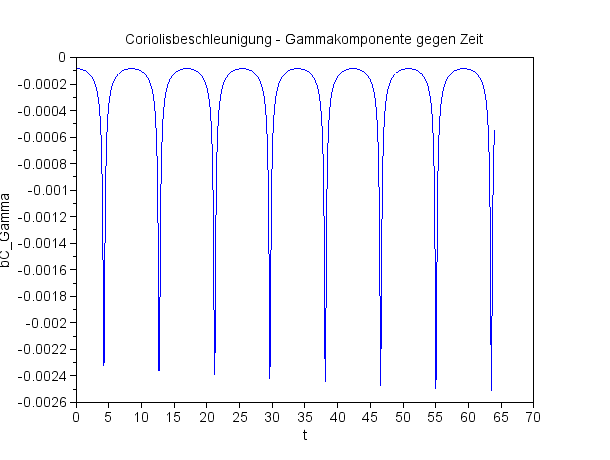
Der Anfangswert der Winkelgeschwindigkeit chiDot ist größer als null
|
Breite 90° Pendellänge 67 m Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
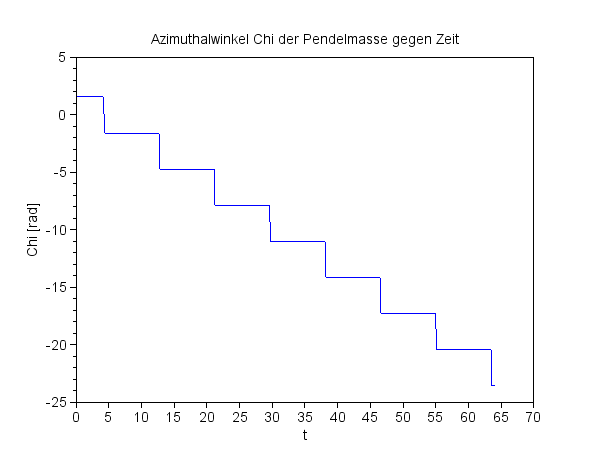
Der Azimuthwinkel Chi 'springt'
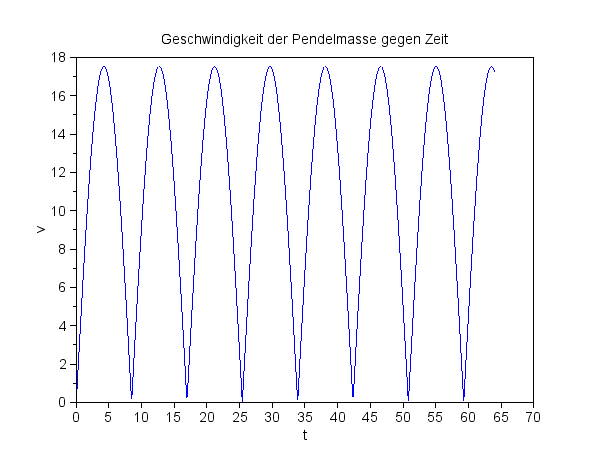
Die Geschwindigkeit der Pendelmasse
|
Wenn die Pendelmasse 'unten durch' schwingt und ihre Geschwindigkeit am größten ist, macht der berechnete Wert des Azimuthwinkels einen Sprung um rund 180° (Werte in Grad): |
+89,938676 +89,906791 +89,827168 +89,285631 -89,599653 -89,832348 -89,889528 |
|
Die Änderungsgeschwindigkeit des Auslenkungswinkels γ macht ebenfalls Sprünge (Werte in Grad/s) und die sind wohl ursächlich: |
-14,933621 -14,974019 -14,991439 +14,988929 +14,963899 +14,916739 |
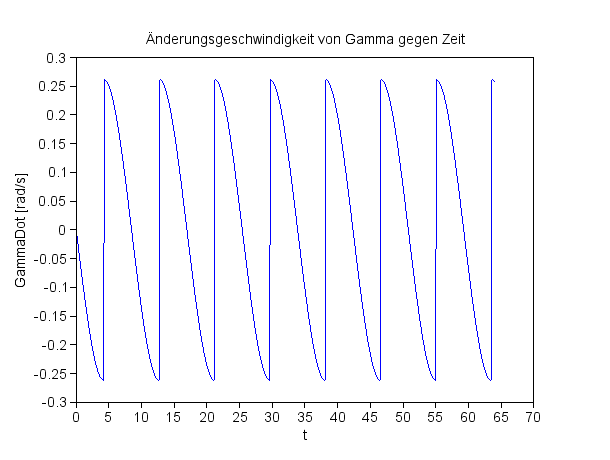
Die Änderungsgeschwindigkeit des Auslenkungswinkels Gamma
|
Die Bewegungsgleichungen am Pol sind: |
|
|
Rotiert die Erde nicht, verschwindet (!) der harte Sprung. Schön. Ansonsten haben die Werte die gleiche Größenordnung. |
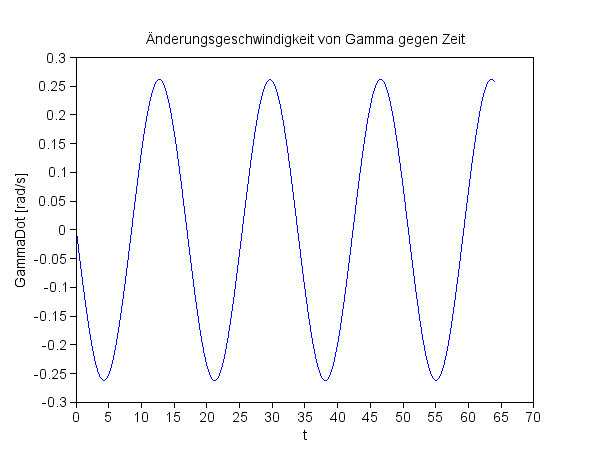
Die Änderungsgeschwindigkeit von Gamma ohne die Erdrotation
|
Breite 90° Pendellänge 67 m >Pendelmasse 28 kg Periodenzeit 16,4 s Zeitintervall 64 s |
|
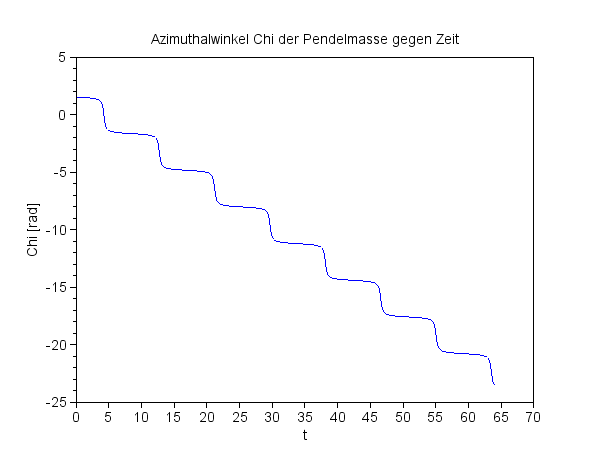
Die Treppe weicht auf ...
|
Das Pendel schwingt nun mit
einem Anfangswert
|
|
|
||
| © 2014 Bernd Ragutt
Alle Rechte vorbehalten |

|
letzte Änderung: 06.07.2020 Kruschtkiste |
|
|
||
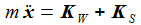
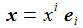
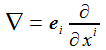
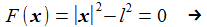
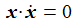
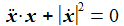
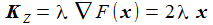
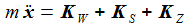
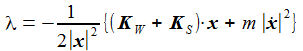
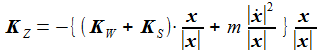
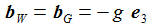

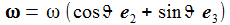
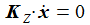
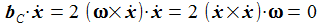
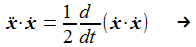
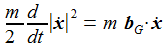
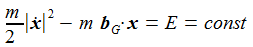
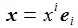
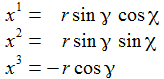
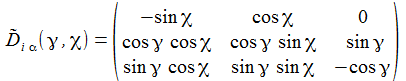
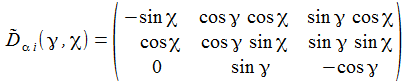
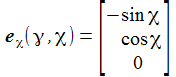
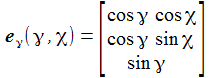
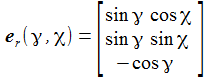
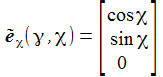
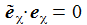
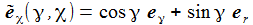
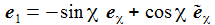
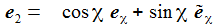
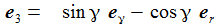
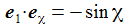
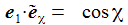
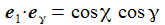
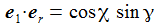
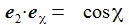
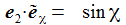
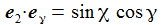
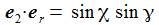
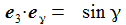
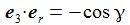
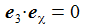
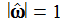
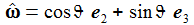
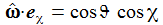
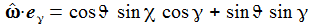
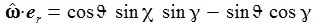
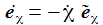
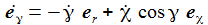
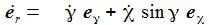
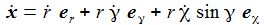
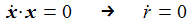
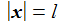
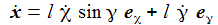
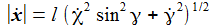

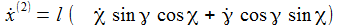
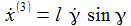
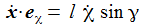
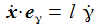
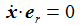
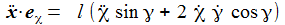
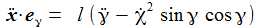
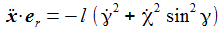
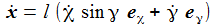
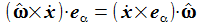
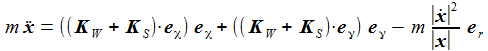
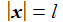
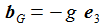
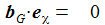
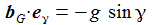
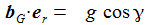
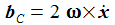
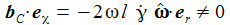
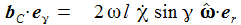
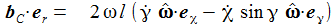
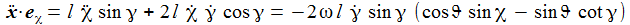
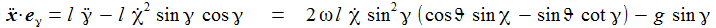
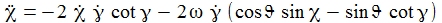
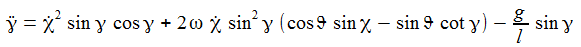
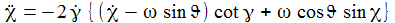
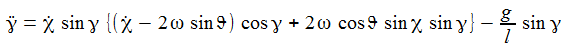
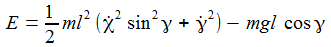
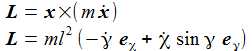
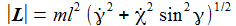
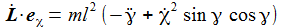
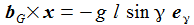
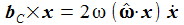
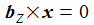
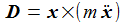
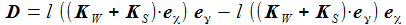
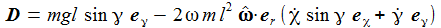
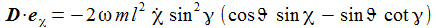
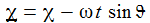
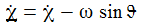
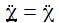
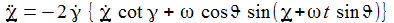
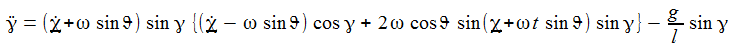
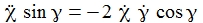
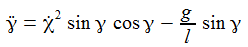
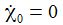
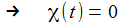
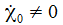
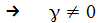
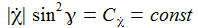
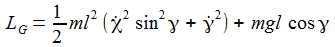
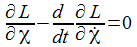
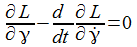
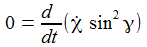 =>
=>
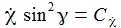
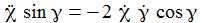
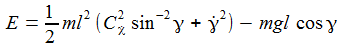
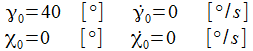
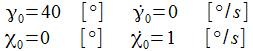
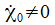 ist, gibt es sozusagen eine Phasensprung, die Phasendiagramme
bekommen ein gänzlich anderes Gesicht.
ist, gibt es sozusagen eine Phasensprung, die Phasendiagramme
bekommen ein gänzlich anderes Gesicht.
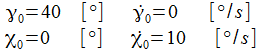
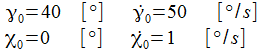
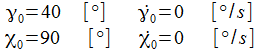
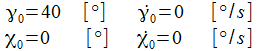
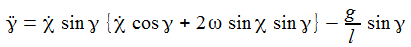
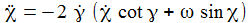
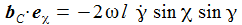
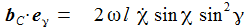
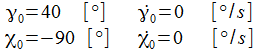
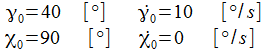
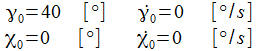
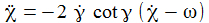
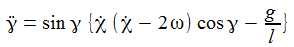
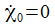 )
mit Werten der Größenordnung 1
in Beziehung setzt:
)
mit Werten der Größenordnung 1
in Beziehung setzt:
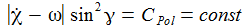
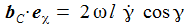
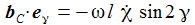
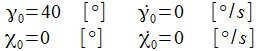
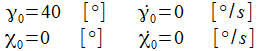
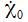 nun
'klein' und/oder die auslenkende Kraft ist wie in unserem Falle
ebenfalls klein, so muss man mit numerischen Problemen beim Lösen
der Differentialgleichungen
im Umfeld γ≈0
rechnen, etwa weil die wirksame Kraft zu Änderungen führt,
die nur in der Größenordnung der Ungenauigkeit des
numerischen Verfahrens liegen.
nun
'klein' und/oder die auslenkende Kraft ist wie in unserem Falle
ebenfalls klein, so muss man mit numerischen Problemen beim Lösen
der Differentialgleichungen
im Umfeld γ≈0
rechnen, etwa weil die wirksame Kraft zu Änderungen führt,
die nur in der Größenordnung der Ungenauigkeit des
numerischen Verfahrens liegen.
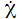 'hinreichend'
groß ist, wird man 'unbesehen' dem Ergenis vertrauen können.
'hinreichend'
groß ist, wird man 'unbesehen' dem Ergenis vertrauen können.
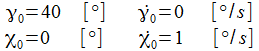
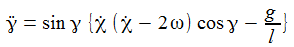
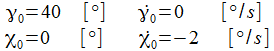
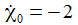 .
Der Verlauf bleibt so, auch wenn die
Rotationsgeschwindigkeit der
Erde auf Null gesetzt wird.
.
Der Verlauf bleibt so, auch wenn die
Rotationsgeschwindigkeit der
Erde auf Null gesetzt wird.