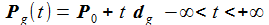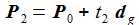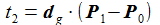|
|
Kleine Sachen mit Python'Ray Tracing' mit sektorierten Segmenten |
|
|
Etwas schlichte Geometrie
|
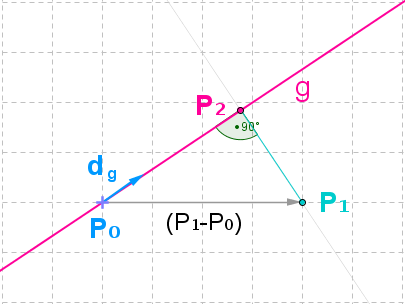
Geraden lassen sich mathematisch auf vielfältige Weise beschreiben. Meine Wahl zielt auf die Einfachheit der Beschreibung: Ich beschreibe eine Gerade durch einen beliebigen Punkt P0, Startpunkt genannt, und durch einen normierten Richtungsvektor dg der Länge 1, der eine der beiden Richtungen der Geraden nach Belieben auszeichnet. In der Skizze unten sind beide Objekte blau eingefärbt. Mit dieser Beschreibungsweise gibt es keine Sonderfälle wie die senkrechte Gerade mit der Steigung ∞, es gibt keine häßlichen Winkel und keine Winkelfunktionen - das Ganze ist einfach und unmittelbar anschaulich, eben Geometrie. |
|
|
Die Punkte Pg auf der Geraden g werden durch eine Parametergleichung definiert: |
|
|
Der Parameter t hat die einfache geometrische Interpretation der Länge des Differenzvektors (Pg(t)-P0). Gegeben sei nun ein beliebiger Punkt P1. Gesucht wird der zu P1 nächstgelegene Punkt P2, der auf der Geraden g liegt. |
|
|
|
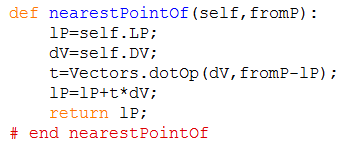
Diesen Geradenpunkt P2 bestimme ich, indem ich den Differenzvektor (P1-P0) auf die Gerade g projiziere, um den Vektor (P2-P0) zu erhalten und damit als Endpunkt dieses Vektors den gesuchten Punkt P2, der als Geradenpunkt die Geradengleichung mit einem Parameter t2 erfüllt:
Den Parameter t2 berechne ich aus den Ausgangsgrößen mithilfe des Skalarproduktes zwischen Vektoren zu:
|
|
Mein Wunsch war es nun, solch wunderschön einfach aussehenden Gleichungen möglichst Eins zu Eins in Programmcode überführen zu können. Wenn das gelingt, kann ich die mathematischen Gleichungen leicht mit dem Programmcode vergleichen und habe eine häßliche Fehlerquelle weniger, |
|
|
nämlich die des fehlerbehaftete Umsetzens von mathematischen Gleichungen in Programmcode. - Und das gelingt mit Python, dem nebenstehenden Beispiel zu entnehmen! Vectors.dotOp bezeichnet hier das Skalarprodukt zwischen zwei Vektoren. In der Kürze liegt bekanntlich die Würze. |
|
|
Und weiter: Das Auge erkennt sofort, dass der grüne Punkt P1 im Bild oben nicht auf der Geraden g liegt. Wann liegt also ein Punkt P1 auf der Geraden? Dazu berechnet man den zu P1 nächstgelegenen Punkt P2 auf der Geraden, und vergleicht diesen mit dem Ausgangspunkt P1. Wenn nun P1 = P2 erfüllt ist, genau dann liegt der Ausgangspunkt auf der Geraden. |
|
|
Dazu noch ein Beispiel zur Implementierung. Liegt ein Punkt etwa auf einer Geraden? Die entsprechende Funktion steht nebenan. '==' ist hier die implementierte Vergleichsoperation für zwei Punkte. |
|
|
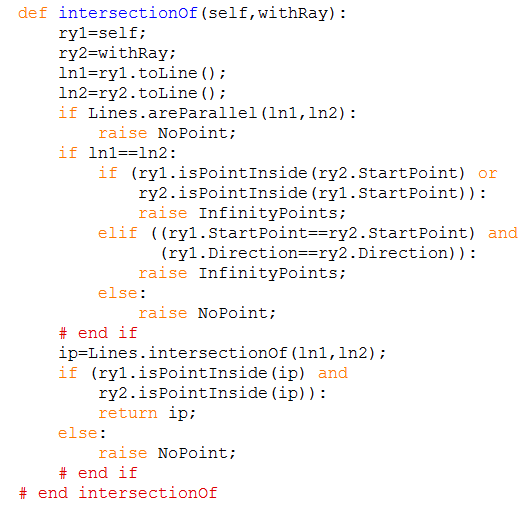
Eine Software-Funktion baut auf der anderen auf. Effizienz spielt keine programmgestaltende Rolle, die Programmsicherheit ist hier das höhere Gut. Und weiter: Strahlen werden durch den ausgezeichneten Startpunkt und einen Richtungvektor beschrieben. Wie erhalte ich den Schnittpunkt zweier Strahlen? In der 'Hauptsache' wie folgt: Ich verlängere die Strahlen zu Geraden und wenn deren Schnittpunkt auf den beiden Ausgangsstrahlen liegt, dann ist das der gewünschte Schnittpunkt der beiden Strahlen. Wie man am Code-Beispiel unten leicht erkennen kann, wird aus der Hauptsache schnell eine Nebensache, die Spezialfälle NoPoint und InfinityPoints machen die Arbeit und den Test aus. Aber dennoch: Man braucht keine Winkelfunktion atan2 und keinen Winkelwirrwar, um das Problem mit einigen Skizzen und Tests zu durchdringen. |
|
|
|
|
|
Und weiter: Ein Segment, also eine Strecke wird durch zwei Punkte bestimmt. Wann liegt ein Punkt auf einer Strecke? Ich verlängere die Strecke zunächst zu zwei Strahlen, in beide Richtungen, sodass die Strecke auch auf beide Strahlen liegt. Wenn der Punkt nun auf den beiden so erzeugten Strahlen liegt, so liegt er auch auf der Strecke. Ganz einfach ist das. Zuletzt: Wann schneidet ein Strahl eine Strecke? Ich verlängere die Strecke in beide Richtungen zu zwei Strahlen und untersuche nun das Schnittverhalten der drei Strahlen. Das Eine baut auf dem Anderen auf. Es entsteht eine Hierachie von einfachen Funktionen. Der Test wird so zum Kinderspiel. |
|
|
Mathematk macht Spaß. Nicht jeder hat in der Schule aufgepasst. Ich hatte einige gute Lehrer. Die moderne, koordinatenfreie Vektorrechnung war damals eine Offenbarung und wirklich etwas fürs Leben. Herrn Rumberger sei gedankt. |
Hier habe ich in einer Handreichung ein kleines mathematisches Grundgerüst zusammen getragen, erstellt mit LibreOffice Writer & Draw.
⇒
Vektoren, Punkte und mehr
|
Wie hilft mir die Sprache Python?
|
Python hilft mir weitaus mehr als ich zunächst erwartet hatte, denn ich hatte Python bisher nur als klassenlose Skriptsprache eingesetzt. Und weiter: Geometrische Objekte werden zu Klassen, eingebaute Funktionen lassen sich überlagern, sodass sich etwa zum Vergleich von Punkten der Operator '==' (intern '__eq__') und zur Differenzbildung von Punkten der Operator '-' (intern: '__sub__') verwenden lässt. Ich hätte gerne für die Multiplikation eines Vektors mit einem Skalar, etwa 2*v oder auch v*2, und für das Skalarprodukt zweier Vektorn, etwa v1*v2, eben auch das Operator-Symbol '*' (intern: '__rmul__') verwendet, Python hat sich aber bisher gestreubt. Deshalb gibt es halt die Funktion dotOp. Ich bin zufrieden damit. |
|
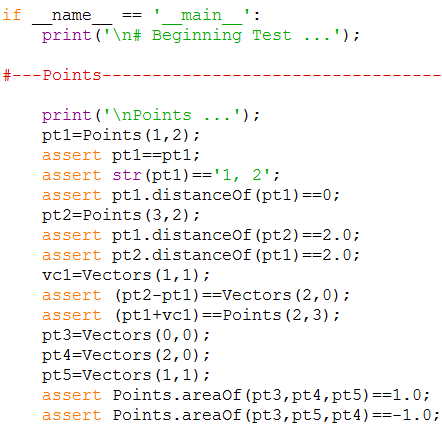
Die Klasse Points ist ganz übersichtlich (siehe unten). Eine Instanz oder ein Objekt p mit den Koordinaten x=1, y=1 wird mit der Anweisung p=Points(1,1) erzeugt, wobei die interne Funktion '__init__' ausgeführt wird. |
|
|
|
|
|
Ich schließe, ganz der konservativ Programmierer, Zeilen mit einem Semikolon und längere Blöcke mit einem Kommentar ab, dann fällt der Code optisch nicht so auseinander. Auf Unterstriche in den Bezeichnern verzichte ich und wo weißer Raum nicht nötig ist, lasse ich ihn weg. Das ist die dichte Packung des Codes, die ich mir bei SciLab angewöhnt habe. (Am Rande: Ich halte es immer noch eine recht abstruse Idee, die Syntax an weißen Raum zu binden. Ich habe mehrere Anläufe gebraucht, um mich daran zu gewöhnen.) Man verschiebt einen Punkt im Raum, hier in der Ebene, durch die Addition eines Vektors, etwa P2=P1+v, dabei wird intern die Funktion '__add__' aufgerufen. Nützlich finde ich auch die Möglichkeit, bei (im Argument) symmetrischen Funktionen einen klassischen Funktionsaufruf verwenden zu können; ein Beispiel für den Abstand zweier Punkte: distance=Points.distanceOf(p1,p2); sieht gut aus, denn die beiden Punkte tauchen in der gleichen Weise als Funktionsparameter auf, aber distance=p1.distanceOf(p2); verletzt die Symmetrie der Funktion und entfernt sich von der mathematischen Schreibweise zu sehr, der eine Punkt taucht als Objekt auf, der andere als Funktionsparameter. |
|
|
Sehr nützlich und hilfreich ist die Möglichkeit, ein Modul sofort als Hauptprogramm ausführen zu können. Daher braucht man bei überschaubaren Modulen kein eigenständiges Testprogramm, man kann den Testcode gleich im Modul unterbringen. So gehen Implementierung und Test eine enge Verbindung ein. Und ich finde es eine sehr gute Idee, den Testcode beim Modul zu belassen. Bei den vielen Freiheiten, die Python zulässt, ist das ein Schritt auf dem Weg zu robuster Software. Ein wenig mehr der Typsicherheit wäre eigentlich nicht schlecht. Ada nimmt da eine extreme Seite ein, Python bietet ein anderes Extrem. |
|
|
Sind die Module umfangreicher, ist es empfehlenswerter, für den Modultest gleich ein Testmodul zu schreiben und sich dabei vom ‚Unit Testing Framework’ Pythons unterstützen zu lassen. Man implementiert kleine Testroutinen, den Testtreiber stellt Python bereit. Das ist unkompliziert und herrlich unaufwändig. |
|
|
Und der statischen Typsicherheit kann man - wenn denn gewünscht - auch ein wenig auf die Sprünge helfen: Da gibt es ja die Funktionsannotationen und seit der Python-Version 3.5 das Modul ‚typing’. PyCharm meckert sogar bei Unstimmigkeiten, ich bin begeistert. |
|
|
Ich habe mich aus Neugier ein paar Wochen lang mit Haskell befasst; dessen starkes Typsystem fand ich elegant, es hat mich beeindruckt. Aber ein paar Wochen reichen bei Haskell leider nicht aus, um diese rein funktionale Programmmiersprache hinreichend zu beherrschen und auch elegant einsetzen zu können. Das war die Chance für Python, der syntaktische weißen Raum war nun nicht mehr so ganz befremdlich! |
|
Hilft mir das Werkzeug «PyCharm»?
|
Manchmal ist man einfach zu genügsam! Ich hatte mich zwar dereinst nach einer zeitgemäßen Entwicklungsumgebung für Python umgeschaut, wurde aber nicht so recht fündig und begnügte mich dann lange mit dem schlichten Editor «Idle» aus dem Python-Installationspaket. Eine Kollegin in Sachen Ada aus alte Tagen machte mich im letzten Jahr so nebenbei auf «PyCharm» aufmerksam. Was einen denn auch gleich erfreut: Eine ‚Community Edition’ des Werkzeugs wird ins Netz gestellt, ein feiner Zug von «JetBrains». Mein erster Eindruck von PyCharm war, dass da zuviel der Meckerei sei — und es gelang mir einfach nicht, die Schriftgröße des Editors zu ändern, was mich doch sehr ärgerte. Nach einigen Wochen habe ich mir das Werkzeug noch einmal vorgenommen: Und siehe da, bald waren die Meckereien wegkonfiguriert und die Schrift sperrte sich auch nicht mehr gegen ein Vergrößern; und mein häusliches «Mercurial» wird sogar ohne Umstände ins Werkzeug eingebaut! Es ist alles dabei, was das Entwicklerherz begehrt: Eine moderne, integrierte Entwicklungsumgebung haben wir da an der Hand, die nichts kostet und die wirklich hilft — nie, nie mehr das allzuschlichte Idle! In der Tat, PyCharm macht mich zur Zeit mächtig an, ich habe meinen gesamten Python-Code einer strengen Revision unterzogen - ja, es ist schon erschreckend, welch schrägen Code der Python-Interpreter mit dem richtigen Ergebnis ausführt. Allerdings konnte ich mich nicht durchringen, endlich den Stil-Standard von Python (PEP 0008) anzuwenden. Deshalb sieht mein Code immer noch so aus, wie ich ihn hier präsentiere, schlicht nicht standardkonform - ich nenne es die hoch verdichtete Form; Leerraum und Unterstriche stören in meinen Augen die Wohlgestalt meines Python-Codes :-) |
Die Anwendung – Ein Beispiel aus der Praxis
|
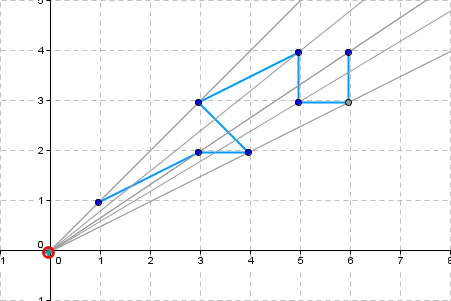
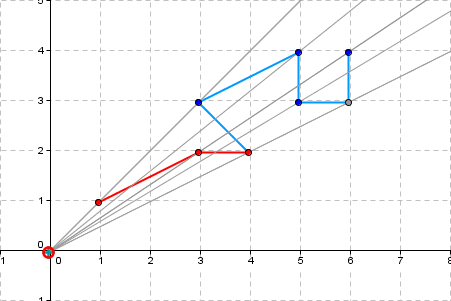
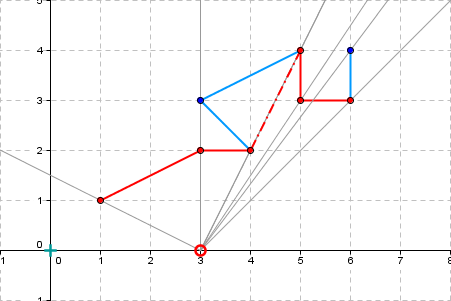
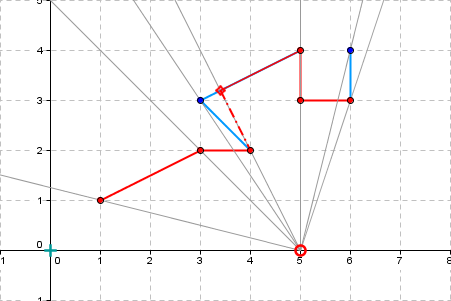
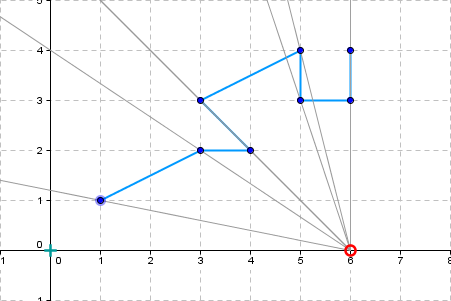
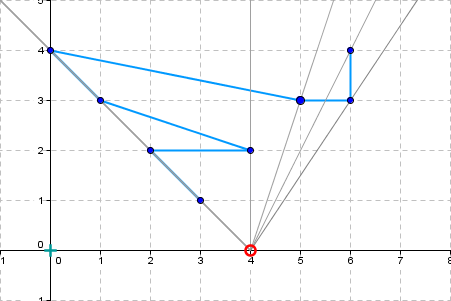
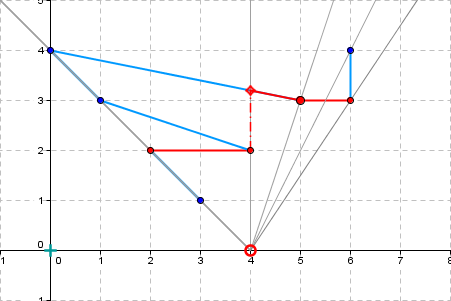
Ein Bewohner von Flachland möchte einen Teil eines Polygonzuges gekennzeichnet haben. Die Teilstücke des gegebenen Polygonzuges sollen sich nicht überschneiden dürfen. Der Bewohner spezifizierte den gewünschten Bereich auf mehr als zwei Seiten mit Hilfe von Pseudocode und Winkeln und Winkelfunktionen - ein großer, häßlicher Haufen undurchschaubarer Algorithmik! Ich hielt dagegen: Ein geometrisches Problem müsse man mit Geometrie und nicht mit Algorithmen in Pseudocode angehen. Es brauchte einige Überzeugungsarbeit, für deren Vorbereitung ich vierzehn Tage Weihnachtsurlaub (2004 / 2005) gerne opferte. Dann war es geschafft! Meine Spezifikation des Problems war es, eben den für den Bewohner sichtbaren Teil des Polygonzuges zu finden. Dieser eine Satz reicht vollständig aus, mehr braucht es nicht. Der geometrische Algorithmus als Anleitung für die Implementierung geht dann so: Man zerlege den Polygonzug in Segmente (Teilstücke), auf dass alle Segmente Sektoren zugeordnet werden können. Dann entnehme man jedem Sektor das Segment, das dem Beobachter am nächsten ist – und schon hat man den sichtbaren Bereich in den Händen. Mit etwas Geometrie, gegossen in Python, und den Listen von Python ist die Implementierung auch schnell erledigt. Ich spendiere mir noch zwei Testfälle: Ein Polygonzug, der von unterschiedlichen Standorten betrachtet wird und ein zweiter, der für einen Sonderfall steht, hier liegen Segmente auf Sektorgrenzen. Der rote Kringel mimt den Beobachter, der vom Beobachter aus der sichtbare Teil ist rot eingefärbt. Die Grafiken habe ich mit «GeoGebra» erstellt. |
|
PolygonTrain points: 3 1 | 2 2 | 4 2 | 3 3 | 1 3 | 0 4 | 5 3 | 6 3 | 6 4 | |
|
|
|
|
|
Observer position: 0 0 |
Visible part - points: 3 4 2 | 3 2 | 1 1 |
|
|
|
|
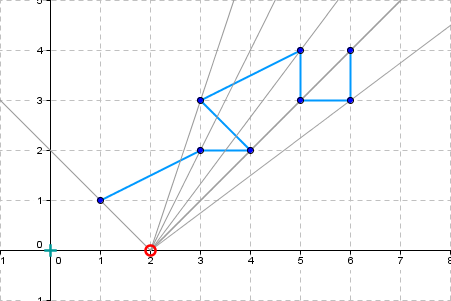
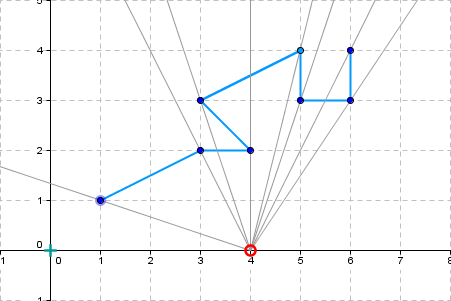
Observer position: 2 0 |
Visible part - points: 5 6 3 | 5 3 | 4 2 | 3 2 | 1 1 |
|
|
|
|
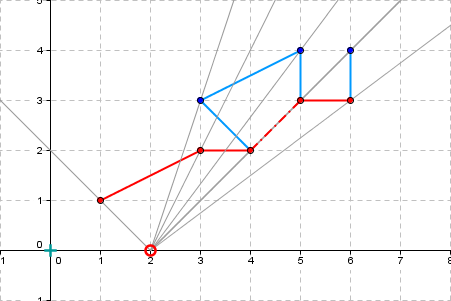
Observer position: 3 0 |
Visible part - points: 6 6 3 | 5 3 | 5 4 | 4 2 | 3 2 | 1 1 |
|
|
|
|
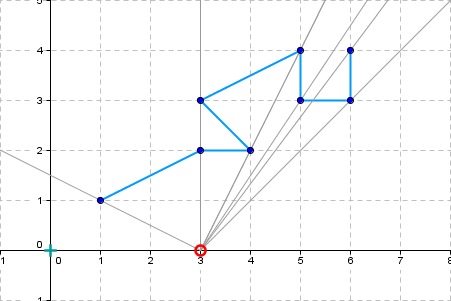
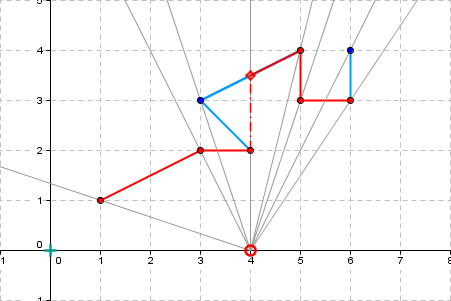
Observer position: 4, 0 |
Visible part - points: 7 6 3 | 5 3 | 5 4 | 4.0 3.5 | 4 2 | 3 2 | 1 1 |
|
|
|
|
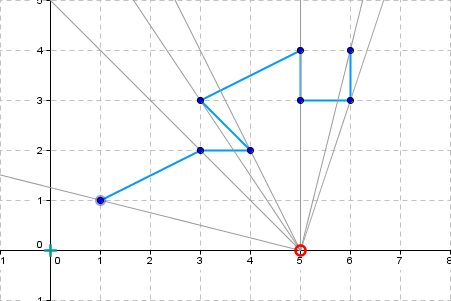
Observer position: 5 0 |
Visible part - points: 7 6 3 | 5 3 | 5 4 | 3.4 3.2 | 4 2 | 3 2 | 1 1 |
|
|
|
|
Observer position: 6 0 |
Visible part - points: 7 6 3 | 5 3 | 4.71 3.86 | 3 3 | 4 2 | 3 2 | 1 1 |
|
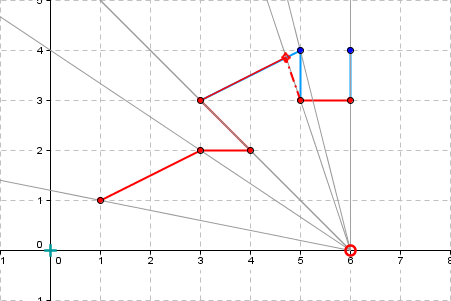
PolygonTrain points: 3 1 | 2 2 | 4 2 | 1 3 | 0 4 | 5 3 | 6 3 | 6 4 | |
|
|
|
|
|
Observer position: 4 0 |
Visible part - points: 5 6 3 | 5 3 | 4.0 3.2 | 4 2 | 2 2 |
Eine kleine Widmung
|
Ich widme die obige Bildkomposition
aus vierzehn handgefertigten Einzelbildern
Es waren wirklich hitzige Diskussionen damals vor fast zehn Jahren. |
----------------------
-- local Nearest_Point
----------------------
-- this function returns the nearest point
-- to point P on ray R
-- this point is
-- a) the orthogonal projection of the
-- point on the ray or
-- b) the start point of the ray
-- (if no projection is possible
--
-- a) b)
-- R R
-- ^ ^
-- | |
-- P | |
-- *-----+ Pi |
-- | |
-- | + Sp
-- * Sp P
-- *
-- return Pi return Sp
--
----------------------
|
||
|
|
||
|
Ach ja, zu guter Letzt sei noch
eine kleine Anmerkung nachgeschoben:
Aber die komplexe Software läuft dennoch |
||
|
|
||
Der Quellcode für Python 3.5
|
Handreichung |
||
|
|
||
|
© 2015 Bernd Ragutt Alle Rechte vorbehalten |

|
letzte Änderung: 21. März 2018 Kruschtkiste |
|
|
||